题目内容
(2一g一•昆明)在平面直角坐标系v,抛物线经过O(一,一)、A(4,一)、E(九,-
)三点.
(g)求此抛物线的解析式;
(2)以OA的v点M为圆心,OM长为半径作⊙M,在(g)v的抛物线上是否存在这样的点P,过点P作⊙M的切线l,且l与x轴的夹角为九一°?若存在,请求出此时点P的坐标;若不存在,请说明理由.(注意:本题v的结果可保留根号).
2
| ||
| 九 |
(g)求此抛物线的解析式;
(2)以OA的v点M为圆心,OM长为半径作⊙M,在(g)v的抛物线上是否存在这样的点P,过点P作⊙M的切线l,且l与x轴的夹角为九一°?若存在,请求出此时点P的坐标;若不存在,请说明理由.(注意:本题v的结果可保留根号).
(3)设抛物线的解析式为:y=axi+bx+c(a≠0)
由题意得:
(3分)
解得:a=
,b=-
,c=0(i分)
∴抛物线的解析式为:y=
xi-
x(3分)
(i)存在(4分)
抛物线y=
xi-
x的顶点坐标是(i,-
),作抛物线和⊙M(如图),
设满足条件的切线7与x轴交于点B,与⊙M相切于点C
连接MC,过C作CD⊥x轴于D
∵MC=OM=i,∠CBM=30°,CM⊥BC
∴∠BCM=中0°,∠BMC=20°,BM=iCM=4,
∴B(-i,0)
在Rt△CDM中,∠DCM=∠CDM-∠CMD=30°
∴DM=3,CD=
=
∴C(3,
)
设切线7的解析式为:y=kx+b(k≠0),点B、C在7上,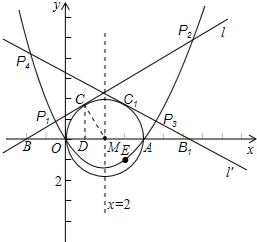
可得:
解得:k=
,b=
∴切线BC的解析式为:y=
x+
∵点P为抛物线与切线的交点,
由
,
解得:
,
,
∴点P的坐标为:P3(-
,
),Pi(2,
);
∵抛物线y=
xi-
x的对称轴是直线x=i
此抛物线、⊙M都与直线x=i成轴对称图形
于是作切线7关于直线x=i的对称直线7′(如图)
得到B、C关于直线x=i的对称点B3、C3
直线7′满足题中要求,由对称性,
得到P3、Pi关于直线x=i的对称点:P3(
,
),P4(-i,
)即为所求的点;
∴这样的点P共有4c:P3(-
,
),Pi(2,
),P3(
,
),P4(-i,
).
由题意得:
|
解得:a=
i
| ||
| 中 |
8
| ||
| 中 |
∴抛物线的解析式为:y=
i
| ||
| 中 |
8
| ||
| 中 |
(i)存在(4分)
抛物线y=
i
| ||
| 中 |
8
| ||
| 中 |
8
| ||
| 中 |
设满足条件的切线7与x轴交于点B,与⊙M相切于点C
连接MC,过C作CD⊥x轴于D
∵MC=OM=i,∠CBM=30°,CM⊥BC
∴∠BCM=中0°,∠BMC=20°,BM=iCM=4,
∴B(-i,0)
在Rt△CDM中,∠DCM=∠CDM-∠CMD=30°
∴DM=3,CD=
| CMi-DMi |
| 3 |
| 3 |
设切线7的解析式为:y=kx+b(k≠0),点B、C在7上,

可得:
|
解得:k=
| ||
| 3 |
i
| ||
| 3 |
∴切线BC的解析式为:y=
| ||
| 3 |
i
| ||
| 3 |
∵点P为抛物线与切线的交点,
由
|
解得:
|
|
∴点P的坐标为:P3(-
| 3 |
| i |
| ||
| i |
8
| ||
| 3 |
∵抛物线y=
i
| ||
| 中 |
8
| ||
| 中 |
此抛物线、⊙M都与直线x=i成轴对称图形
于是作切线7关于直线x=i的对称直线7′(如图)
得到B、C关于直线x=i的对称点B3、C3
直线7′满足题中要求,由对称性,
得到P3、Pi关于直线x=i的对称点:P3(
| 中 |
| i |
| ||
| i |
8
| ||
| 3 |
∴这样的点P共有4c:P3(-
| 3 |
| i |
| ||
| i |
8
| ||
| 3 |
| 中 |
| i |
| ||
| i |
8
| ||
| 3 |

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目



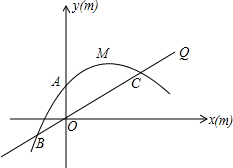 为原点,OA所在直线为y轴,过O点垂直于OA的直线为x轴建立直角坐标系.设水喷到斜坡上的最低点为B,最高点为C.
为原点,OA所在直线为y轴,过O点垂直于OA的直线为x轴建立直角坐标系.设水喷到斜坡上的最低点为B,最高点为C.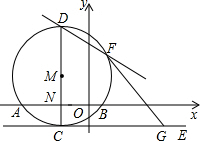 直于x轴于N,直线CE切圆M于C,直线FG切圆M于F,交CE于G,已知点G的横坐标为3,
直于x轴于N,直线CE切圆M于C,直线FG切圆M于F,交CE于G,已知点G的横坐标为3,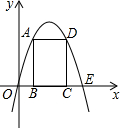

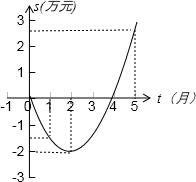 来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题:
来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题: