题目内容
大润发超市进了一批成本为8元/个的文具盒．调查发现：这种文具盒每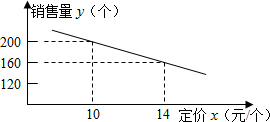
个星期的销售量y（个）与它的定价x（元/个）的关系如图所示：
（1）求这种文具盒每个星期的销售量y（个）与它的定价x（元/个）之间的函数关系式（不必写出自变量x的取值范围）；
（2）每个文具盒定价是多少元时，超市每星期销售这种文具盒（不考虑其他因素）可获得的利润最高？最高利润是多少？
个星期的销售量y（个）与它的定价x（元/个）的关系如图所示：（1）求这种文具盒每个星期的销售量y（个）与它的定价x（元/个）之间的函数关系式（不必写出自变量x的取值范围）；
（2）每个文具盒定价是多少元时，超市每星期销售这种文具盒（不考虑其他因素）可获得的利润最高？最高利润是多少？
（1）设y=kx+b
由题意得：
，
解之得：k=-10；b=300．
∴y=-10x+300．
（2）由上知超市每星期的利润：W=（x-8）•y=（x-8）（-10x+300）
=-10（x-8）（x-30）=-10（x2-38x+240）
=-10（x-19）2+1210
答：当x=19即定价19元/个时超市可获得的利润最高．
最高利润为1210元．
由题意得：
|
解之得：k=-10；b=300．
∴y=-10x+300．
（2）由上知超市每星期的利润：W=（x-8）•y=（x-8）（-10x+300）
=-10（x-8）（x-30）=-10（x2-38x+240）
=-10（x-19）2+1210
答：当x=19即定价19元/个时超市可获得的利润最高．
最高利润为1210元．
练习册系列答案
阅读快车系列答案
相关题目
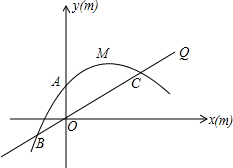为原点，OA所在直线为y轴，过O点垂直于OA的直线为x轴建立直角坐标系．设水喷到斜坡上的最低点为B，最高点为C．
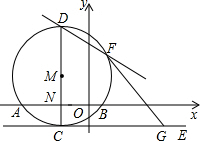直于x轴于N，直线CE切圆M于C，直线FG切圆M于F，交CE于G，已知点G的横坐标为3，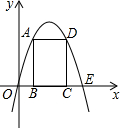
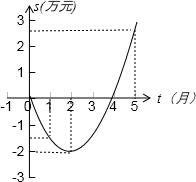来累积利润s（万元）与销售时间t（月）之间的关系（即前t个月的利润总和s和t之间的关系）．根据图象提供的信息，解答下列问题：