题目内容
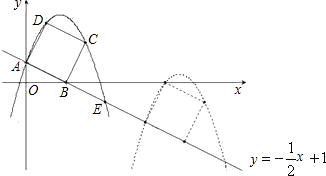
如图1,在平面直角坐标系中,将n个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在x轴和y轴的正半轴上.现将矩形OABC绕点O顺时针旋转,使得点B落到x轴的正半轴上(如图2),设抛物线y=ax2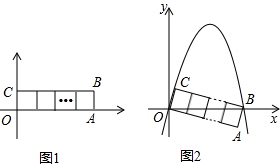 +bx+c(a<0),如果抛物线同时经过点O、B、C:
+bx+c(a<0),如果抛物线同时经过点O、B、C:
①当n=3时a=______;
②a关于n的关系式是______.
 +bx+c(a<0),如果抛物线同时经过点O、B、C:
+bx+c(a<0),如果抛物线同时经过点O、B、C:①当n=3时a=______;
②a关于n的关系式是______.
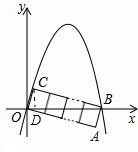
①如图当n=3时,OC=1,BC=3,
设所求抛物线解析式为y=ax2+bx,
过C作CD⊥OB于点D,
则Rt△OCD∽Rt△OBC,
∴
=
=
,
设OD=t,则CD=3t,
∵OD2+CD2=OC2,
∴(3t)2+t2=12,∴t=
=
∴C(
,
),又B(
,0),
∴把B、C坐标代入抛物线解析式,得
解得:a=-
,
故答案为:-
.
②当n=2时,OC=1,BC=2,
∴OB=
,
∴1×2=
CD,B(
,0)
∴CD=
,
∴OD=
,
∴C(
,
)
设所求抛物线解析式为y=ax2+bx,
∴
,
解得:a=-
;
同理当n=4时,a=-
;
∴可以得出a关于n的关系式是:a=-
.
故答案为:-
,a=-
.
设所求抛物线解析式为y=ax2+bx,
过C作CD⊥OB于点D,
则Rt△OCD∽Rt△OBC,
∴
| OD |
| CD |
| OC |
| BC |
| 1 |
| 3 |
设OD=t,则CD=3t,
∵OD2+CD2=OC2,
∴(3t)2+t2=12,∴t=
|
| ||
| 10 |
∴C(
| ||
| 10 |
| 3 |
| 10 |
| 10 |
| 10 |
∴把B、C坐标代入抛物线解析式,得
|
解得:a=-
| ||
| 3 |
故答案为:-
| ||
| 3 |
②当n=2时,OC=1,BC=2,
∴OB=
| 5 |
∴1×2=
| 5 |
| 5 |
∴CD=
2
| ||
| 5 |
∴OD=
| ||
| 5 |
∴C(
| ||
| 5 |
2
| ||
| 5 |
设所求抛物线解析式为y=ax2+bx,
∴
|
解得:a=-
| ||
| 2 |
同理当n=4时,a=-
| ||
| 4 |
∴可以得出a关于n的关系式是:a=-
| ||
| n |

故答案为:-
| ||
| 3 |
| ||
| n |

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目

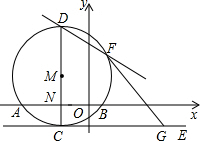 直于x轴于N,直线CE切圆M于C,直线FG切圆M于F,交CE于G,已知点G的横坐标为3,
直于x轴于N,直线CE切圆M于C,直线FG切圆M于F,交CE于G,已知点G的横坐标为3,
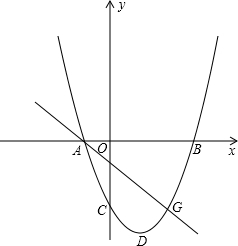 x轴交于A、B两点,其中B点的坐标为(3,0),且OB=OC.
x轴交于A、B两点,其中B点的坐标为(3,0),且OB=OC.