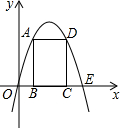题目内容
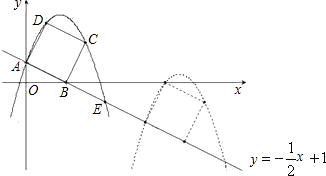
矩形ABCD的边长AB=3,AD=2,将此矩形放在平面直角坐标系中,使AB在x轴的正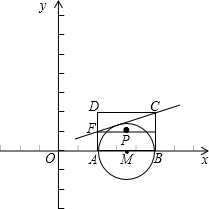 半轴上,点A在点B的左侧,另两个顶点都在第一象限,且直线y=
半轴上,点A在点B的左侧,另两个顶点都在第一象限,且直线y=
x-1经过这两个顶点中的一个.
(1)求A、B、C、D四点坐标;
(2)以AB为直径作⊙M,记过A、B两点的抛物线y=ax2+bx+c的顶点为P.
①若P点在⊙M和矩形内,求a的取值范围;
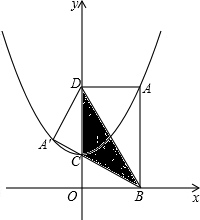
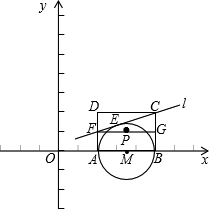
②过点C作CF切⊙M于E,交AD于F,当PF∥AB时,求抛物线的函数解析式.
 半轴上,点A在点B的左侧,另两个顶点都在第一象限,且直线y=
半轴上,点A在点B的左侧,另两个顶点都在第一象限,且直线y=| 3 |
| 2 |
(1)求A、B、C、D四点坐标;
(2)以AB为直径作⊙M,记过A、B两点的抛物线y=ax2+bx+c的顶点为P.
①若P点在⊙M和矩形内,求a的取值范围;
②过点C作CF切⊙M于E,交AD于F,当PF∥AB时,求抛物线的函数解析式.
(1)首先画图.设点A坐标为(x,0)
又∵AB=3,AD=2且点A在点B的左侧.AB在x轴的正半轴上.
又∵ABCD为矩形,则点B、C、D的坐标分别为(x+3,0),(x+3,2),(x,2)
∴直线y=
x-1,经过这两个顶点中的一个.
当其经过点C时,
(x+3)=3
∴x=-1
又∵点A在x轴正半轴上
∴x>0
∴x=-1舍去
当其经过点D时,
x-1=2
∴x=2,符合题意.
∴A、B、C、D四点坐标分别为(2,0)、(5,0)、(5,2)、(2,2)
(2)①∵此抛物线过点A.B
∴可设抛物线的解析式为y=a(x-2)(x-5)=ax2-7ax+10a(a≠0)
∴其顶点P的坐标为(
,-
a)
而⊙M的圆心M的坐标为(
,0),半径为
∴若P点在⊙M和矩形内,则0<-
a<
,
∴-
<a<0.
②设点F坐标为(2,y),则FA=y
∵CF切⊙M于E,CB、FA均为⊙M的切线,
根据切线长定理有CE=BC=2,EF=AF=-
a,
设直线PF与BC相交于G,在直角三角形CFG中,
CF2=FG2+CG2,CG=BC-AF=2+
a,CF=BC+EF=2-
a;
∴(2-
a)2=(2+
a)2+9
解得a=-
∴抛物线的解析式为y=-
(x-2)(x-5)=-
x2+
x-5.

又∵AB=3,AD=2且点A在点B的左侧.AB在x轴的正半轴上.
又∵ABCD为矩形,则点B、C、D的坐标分别为(x+3,0),(x+3,2),(x,2)
∴直线y=
| 3 |
| 2 |
当其经过点C时,
| 3 |
| 2 |
∴x=-1
又∵点A在x轴正半轴上
∴x>0
∴x=-1舍去
当其经过点D时,
| 3 |
| 2 |
∴x=2,符合题意.
∴A、B、C、D四点坐标分别为(2,0)、(5,0)、(5,2)、(2,2)
(2)①∵此抛物线过点A.B
∴可设抛物线的解析式为y=a(x-2)(x-5)=ax2-7ax+10a(a≠0)
∴其顶点P的坐标为(
| 7 |
| 2 |
| 9 |
| 4 |
而⊙M的圆心M的坐标为(
| 7 |
| 2 |
| 3 |
| 2 |
∴若P点在⊙M和矩形内,则0<-
| 9 |
| 4 |
| 3 |
| 2 |
∴-
| 2 |
| 3 |
②设点F坐标为(2,y),则FA=y
∵CF切⊙M于E,CB、FA均为⊙M的切线,
根据切线长定理有CE=BC=2,EF=AF=-
| 9 |
| 4 |
设直线PF与BC相交于G,在直角三角形CFG中,
CF2=FG2+CG2,CG=BC-AF=2+
| 9 |
| 4 |
| 9 |
| 4 |
∴(2-
| 9 |
| 4 |
| 9 |
| 4 |
解得a=-
| 1 |
| 2 |
∴抛物线的解析式为y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |

练习册系列答案
相关题目