题目内容
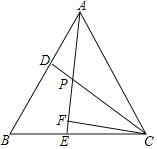
【题目】将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△DEF中,∠EDF=90°,∠E=45°)如图①摆放,点D为AB的中点,DE交AC于点P,DF经过点C.
(1)求∠ADE的度数;
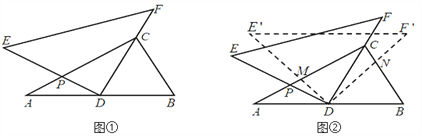
(2)如图②,将△DEF绕点D顺时针方向旋转角![]() ,此时等腰直角三角尺记为
,此时等腰直角三角尺记为![]() ,
, ![]() 交AC于点M,
交AC于点M, ![]() 交BC于点N,试判断
交BC于点N,试判断![]() 的值是否随着
的值是否随着![]() 的变化而变化?如果不变,请求出
的变化而变化?如果不变,请求出![]() 的值;反之,请说明理由.
的值;反之,请说明理由.
【答案】(1)∠ADE=30°;(2)不变化,理由见解析.
【解析】将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△DEF中,∠EDF=90°,∠E=45°)如图①摆放,点D为AB的中点,DE交AC于点P,DF经过点C.
(1)求∠ADE的度数;
(2)如图②,将△DEF绕点D顺时针方向旋转角![]() (0°<
(0°<![]() <60°),此时等腰直角三角尺记为
<60°),此时等腰直角三角尺记为![]() ,
, ![]() 交AC于点M,
交AC于点M, ![]() 交BC于点N,试判断
交BC于点N,试判断![]() 的值是否随着
的值是否随着![]() 的变化而变化?如果不变,请求出
的变化而变化?如果不变,请求出![]() 的值;反之,请说明理由.
的值;反之,请说明理由.

试题分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得CD=AD=BD=![]() AB,根据等边对等角求出∠ACD=∠A,再求出∠ADC=120°,再根据∠ADE=∠ADC-∠EDF计算即可得解;
AB,根据等边对等角求出∠ACD=∠A,再求出∠ADC=120°,再根据∠ADE=∠ADC-∠EDF计算即可得解;
(2)根据同角的余角相等求出∠PDM=∠CDN,再根据然后求出△BCD是等边三角形,根据等边三角形的性质求出∠BCD=60°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CPD=60°,从而得到∠CPD=∠BCD,再根据两组角对应相等,两三角形相似判断出△DPM和△DCN相似,再根据相似三角形对应边成比例可得![]() 为定值.
为定值.
试题解析:(1)∵∠ACB=90°,点D为AB的中点,
∴CD=AD=BD=![]() AB,
AB,
∴∠ACD=∠A=30°,
∴∠ADC=180°-30°×2=120°,
∴∠ADE=∠ADC-∠EDF=120°-90°=30°;
(2)不变化.
∵∠EDF=90°,
∴∠PDM+∠E′DF=∠CDN+∠E′DF=90°,
∴∠PDM=∠CDN,
∵∠B=60°,BD=CD,
∴△BCD是等边三角形,
∴∠BCD=60°,
∵∠CPD=∠A+∠ADE=30°+30°=60°,
∴∠CPD=∠BCD,
在△DPM和△DCN中,
![]() ,
,
∴△DPM∽△DCN,
∴![]() ,
,
∵![]() =tan∠ACD=tan30°=
=tan∠ACD=tan30°=![]() ,
,
∴![]() 的值不随着α的变化而变化,是定值
的值不随着α的变化而变化,是定值![]() .
.