题目内容
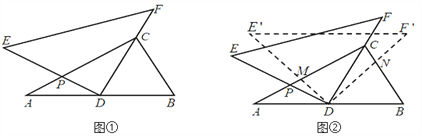
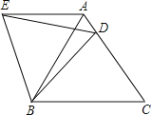
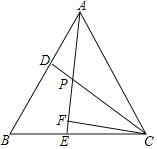
【题目】等边三角形ABC中,D、E分别是AB、BC上的点,且AD=BE,AE、CD相交于点P,CF⊥AE.
(1)求∠CPE的度数;
(2)求证:PF=![]() PC.
PC.
【答案】(1)∠CPE=60°;(2)见详解.
【解析】
(1)先根据已知条件判定出△BEA≌△CAD,得到CD=AE,再结合已知可证△CDB≌△ACE,由此可得∠AEC十∠CPE+∠PCE=∠BDC+∠PCE+∠B,即可知∠B=∠CPE=60°;
(2)由CF⊥AE,∠CPE=60°,可得△CPF是含30°角的直角三角形,即可证明.
(1)∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠B,
又∵AD=BE,
∴△BEA≌△CAD,BD=CE,
∴CD=AE,
又∵∠ACB=∠B,
∴△CDB≌△ACE,
∴∠BDC=∠AEC,
∴∠AEC十∠CPE+∠PCE=∠BDC+∠PCE+∠B,
∴∠B=∠CPE=60°;
(2)∵CF⊥AE,∠CPE=60°,
∴∠FCP=30°,
∴PF=![]() PC.
PC.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
【题目】某校随机选取了![]() 名学生,对他们喜欢的运动项目进行调查,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.
名学生,对他们喜欢的运动项目进行调查,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.
项目 | 长跑 | 短跑 | 跳绳 | 跳远 |
200 | √ | × | √ | √ |
300 | × | √ | × | √ |
150 | √ | √ | √ | × |
200 | √ | × | √ | × |
150 | √ | × | × | × |
(1)估计该校学生同时喜欢短跑和跳绳的概率;
(2)估计该校学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;