题目内容
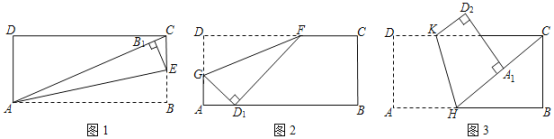
【题目】如图,已知在Rt△ABC中,∠ACB=90°,AC > BC,CD是Rt△ABC的高,E是AC的中点,ED的延长线与CB的延长线相交于点F.
(1)求证:DF是BF和CF的比例中项;
(2)在AB上取一点G,如果AE·AC=AG·AD,求证:EG·CF=ED·DF.

【答案】证明见解析
【解析】试题分析:(1)根据已知求得∠BDF=∠BCD,再根据∠BFD=∠DFC,证明△BFD∽△DFC,从而得BF:DF=DF:FC,进行变形即得;
(2)由已知证明△AEG∽△ADC,得到∠AEG=∠ADC=90°,从而得EG∥BC,继而得![]() ,
,
由(1)可得![]() ,从而得
,从而得![]() ,问题得证.
,问题得证.
试题解析:(1)∵∠ACB=90°,∴∠BCD+∠ACD=90°,
∵CD是Rt△ABC的高,∴∠ADC=∠BDC=90°,∴∠A+∠ACD=90°,∴∠A=∠BCD,
∵E是AC的中点,
∴DE=AE=CE,∴∠A=∠EDA,∠ACD=∠EDC,
∵∠EDC+∠BDF=180°-∠BDC=90°,∴∠BDF=∠BCD,
又∵∠BFD=∠DFC,
∴△BFD∽△DFC,
∴BF:DF=DF:FC,
∴DF2=BF·CF;
(2)∵AE·AC=ED·DF,
∴![]() ,
,
又∵∠A=∠A,
∴△AEG∽△ADC,
∴∠AEG=∠ADC=90°,
∴EG∥BC,
∴![]() ,
,
由(1)知△DFD∽△DFC,
∴![]() ,
,
∴![]() ,
,
∴EG·CF=ED·DF.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目