题目内容
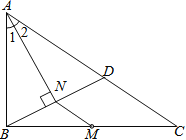
【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四边形ABCD中, , ;
求证:四边形ABCD是平行四边形.

【答案】已知:①③(或①④或②④或③④),证明见解析.
【解析】试题分析:根据平行四边形的判定方法就可以组合出不同的结论,然后即可证明.
其中解法一是证明两组对角相等的四边形是平行四边形;
解法二是证明两组对边平行的四边形是平行四边形;
解法三是证明一组对边平行且相等的四边形是平行四边形;
解法四是证明两组对角相等的四边形是平行四边形.
试题解析:已知:①③,①④,②④,③④均可,其余均不可以.
解法一:
已知:在四边形ABCD中,①AD∥BC,③∠A=∠C,
求证:四边形ABCD是平行四边形.
证明:∵AD∥BC,
∴∠A+∠B=180°,∠C+∠D=180°.
∵∠A=∠C,
∴∠B=∠D.
∴四边形ABCD是平行四边形.
解法二:
已知:在四边形ABCD中,①AD∥BC,④∠B+∠C=180°,
求证:四边形ABCD是平行四边形.
证明:∵∠B+∠C=180°,
∴AB∥CD,
又∵AD∥BC,
∴四边形ABCD是平行四边形;
解法三:
已知:在四边形ABCD中,②AB=CD,④∠B+∠C=180°,
求证:四边形ABCD是平行四边形.
证明:∵∠B+∠C=180°,
∴AB∥CD,
又∵AB=CD,
∴四边形ABCD是平行四边形;
解法四:
已知:在四边形ABCD中,③∠A=∠C,④∠B+∠C=180°,
求证:四边形ABCD是平行四边形.
证明:∵∠B+∠C=180°,
∴AB∥CD,
∴∠A+∠D=180°,
又∵∠A=∠C,
∴∠B=∠D,
∴四边形ABCD是平行四边形.

【题目】某采摘农场计划种植A,B两种草莓共6亩,根据表格信息,解答下列问题:
项目 品种 | A | B |
年亩产(单位:千克) | 1200 | 2000 |
采摘价格 | 60 | 40 |
(1)若该农场每年草莓全部被采摘的总收入为460000元,那么A、B两种草莓各种多少亩?
(2)若要求种植A种草莓的亩数不少于种植B种草莓的一半,那么种植A种草莓多少亩时,可使该农场每年草莓全部被采摘的总收入最多?并求出最多总收入.