题目内容
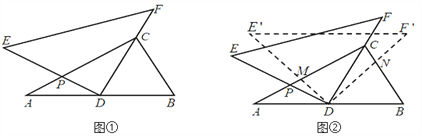
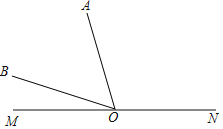
【题目】如图1,点A、O、B依次在直线MN上,现将射线OA绕点O沿顺时针方向以每秒3°的速度旋转,同时射线OB绕点O沿逆时针方向以每秒6°的速度旋转,直线MN保持不动,如图2,设旋转时间为t(0≤t≤60,单位秒)

(1)当t=2时,求∠AOB的度数;
(2)在运动过程中,当∠AOB第二次达到63°时,求t的值;
(3)在旋转过程中是否存在这样的t,使得射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角(指大于0°而小于180°的角)的平分线?如果存在,请求出t的值;如果不存在,请说明理由.
【答案】(1)162°;(2)27;(3)存在,当t的值分别为12、24秒时,射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角的平分线
【解析】
(1)先由题意计算出∠AOM和∠BON的度数,再由∠AOB=180°﹣∠AOM﹣∠BON计算得到答案;
(2)当∠AOB第二次达到63°时,射线OB在OA的左侧,根据∠AOM+∠BON-∠MON=63°列方程求解可得;
(3)射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角的平分线有两种情况:
①OB平分∠AON时,根据∠BON=![]() ∠AON,列方程求解;
∠AON,列方程求解;
②OB平分∠AOM时,根据![]() ∠AOM=∠BOM,列方程求解.
∠AOM=∠BOM,列方程求解.
解:(1)当t=2时,∠AOM=3°×2=6°,∠BON=6°×2=12°,
所以∠AOB=180°﹣∠AOM﹣∠BON=162°;
(2)如图,
根据题意知:∠AOM=3t,∠BON=6t,
当∠AOB第二次达到63°时,∠AOM+∠BON﹣∠MON=63°,
即3t+6t﹣180=63,解得:t=27.
故t=27秒时,∠AOB第二次达到63°.
(3)射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角(大于0°而小于180°)的平分线有以下两种情况:
①OB平分∠AON时,
∵∠BON=![]() ∠AON,
∠AON,
∴6t=![]() (180﹣3t),
(180﹣3t),
解得:t=12;
②OB平分∠AOM时,
∵![]() ∠AOM=∠BOM,
∠AOM=∠BOM,
∴![]() t=180﹣6t,
t=180﹣6t,
解得:t=24.
综上,当t的值分别为12、24秒时,射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角的平分线.

【题目】观察下表:
序号 | 1 | 2 | 3 | … |
图形 |
|
|
| … |
我们把某格中字母和所得到的多项式称为“特征多项式”,例如第1格的“特征多项式”为![]() .
.
回答下列问题:
(1)第3格的“特征多项式”为____________,
第4格的“特征多项式”为____________,
第![]() 格的“特征多项式”为____________;
格的“特征多项式”为____________;
(2)若第1格的“特征多项式”的值为10,第2格的“特征多项式”的值为19,求![]() 的值.
的值.