ЬтФПФкШн
ЁОЬтФПЁПШчЭМ1ЃЌдке§ЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧЖдНЧЯп
ЪЧЖдНЧЯп![]() ЩЯШЮвтвЛЕуЃЈВЛгы
ЩЯШЮвтвЛЕуЃЈВЛгы![]() ЁЂ
ЁЂ![]() жиКЯЃЉЃЌЕу
жиКЯЃЉЃЌЕу![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛжБЯп
НЛжБЯп![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
ГѕВНИажЊЃКЕБЕу![]() гыЕу
гыЕу![]() жиКЯЪБЃЌБШНЯЃК
жиКЯЪБЃЌБШНЯЃК![]()
![]() ЃЈбЁЬюЁА
ЃЈбЁЬюЁА![]() ЁБЁЂЁА
ЁБЁЂЁА![]() ЁБЛђЁА
ЁБЛђЁА![]() ЁБЃЉЃЎ
ЁБЃЉЃЎ
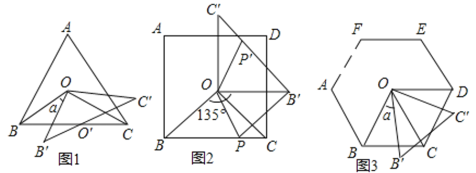
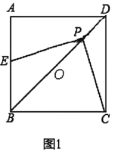
дйДЮИажЊЃКШчЭМ1ЃЌЕБЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЪБЃЌШчКЮХаЖЯ
ЩЯЪБЃЌШчКЮХаЖЯ![]() КЭ
КЭ![]() Ъ§СПЙиЯЕФиЃП
Ъ§СПЙиЯЕФиЃП
МзЭЌбЇЭЈЙ§Й§Еу![]() ЗжБ№Яђ
ЗжБ№Яђ![]() КЭ
КЭ![]() зїДЙЯпЃЌЙЙдьШЋЕШШ§НЧаЮЃЌжЄУїГі
зїДЙЯпЃЌЙЙдьШЋЕШШ§НЧаЮЃЌжЄУїГі![]() ЃЛ
ЃЛ
ввЭЌбЇЭЈЙ§СЌНг![]() ЃЌжЄУїГі
ЃЌжЄУїГі![]() ЃЌ
ЃЌ![]() ЃЌДгЖјжЄУїГі
ЃЌДгЖјжЄУїГі![]() ЃЎ
ЃЎ
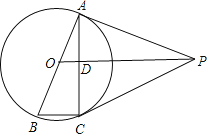
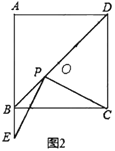
РэЯыИаЮђЃКШчЭМ2ЃЌЕБЕу![]() ТфдкЯпЖЮ
ТфдкЯпЖЮ![]() ЩЯЪБЃЌХаЖЯ
ЩЯЪБЃЌХаЖЯ![]() КЭ
КЭ![]() ЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЭиеЙгІгУЃКСЌНг![]() ЃЌВЂбгГЄ
ЃЌВЂбгГЄ![]() НЛжБЯп
НЛжБЯп![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
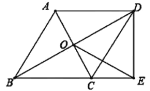
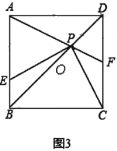
ЃЈ1ЃЉЕБ![]() ЪБЃЌШчЭМ3ЃЌжБНгаДГі
ЪБЃЌШчЭМ3ЃЌжБНгаДГі![]() ЕФУцЛ§ЮЊ ЃЛ
ЕФУцЛ§ЮЊ ЃЛ
ЃЈ2ЃЉжБНгаДГі![]() УцЛ§
УцЛ§![]() ЕФШЁжЕЗЖЮЇ ЃЎ
ЕФШЁжЕЗЖЮЇ ЃЎ
ЁОД№АИЁПГѕВНИажЊЃКЃНЃЛРэЯыИаЮђЃКPEЃНPCЃЌРэгЩМћНтЮіЃЛЭиеЙгІгУЃКЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ0ЃМSЁм
ЃЛЃЈ2ЃЉ0ЃМSЁм![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
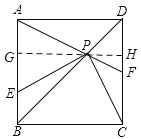
ГѕВНИажЊЃКЕБЕуPгыЕуOжиКЯЪБЃЌдђЕуEгыЕуBжиКЯЃЌИљОне§ЗНаЮЕФаджЪМДПЩЕУЕННсТлЃЛ
РэЯыИаЮђЃКPEЃНPCЃЌЙ§PзїGHЁЭABгкGЃЌНЛCDгкHЃЌгЩЁАAASЁБПЩжЄЁїEGPЁеЁїPHCЃЌПЩЕУНсТлЃЛ
ЭиеЙгІгУЃКЃЈ1ЃЉЭЌРэзїИЈжњЯпПЩжЊЁїEGPЁеЁїPHCЃЌжЄУїЁїDPFЁзЁїBPAЃЌИљОнЯрЫЦШ§НЧаЮЯрЫЦБШЕШгкЖдгІИпЕФБШЕУЃК![]() ЃЌМЦЫуPHЃН
ЃЌМЦЫуPHЃН![]() ЃЌPGЃН
ЃЌPGЃН![]() ЃЌШЛКѓЧѓГіAEЕФГЄЃЌИљОнШ§НЧаЮУцЛ§ЙЋЪНПЩЕУНсТлЃЛ
ЃЌШЛКѓЧѓГіAEЕФГЄЃЌИљОнШ§НЧаЮУцЛ§ЙЋЪНПЩЕУНсТлЃЛ
ЃЈ2ЃЉЩшPHЃНxЃЌдђPGЃН9ЃxЃЌНсКЯжЎЧАЫљЕУЕФНсТлСаГіSЕФКЏЪ§ЙиЯЕЪНЃЌРћгУЖўДЮКЏЪ§ЕФаджЪЧѓЕУSЕФШЁжЕЗЖЮЇМДПЩЃЎ
НтЃКГѕВНИажЊЃКЕБЕуPгыЕуOжиКЯЪБЃЌдђЕуEгыЕуBжиКЯЃЌ
ЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌ
ЁрЁЯBCDЃН90ЁуЃЌ
ЁпЕуOЪЧBDЕФжаЕуЃЌ
ЁрOCЃНOBЃН![]() BDЃЌ
BDЃЌ
МДЃКPCЃНPEЃЌ
ЙЪД№АИЮЊЃКЃНЃЛ
РэЯыИаЮђЃКPEЃНPCЃЌРэгЩШчЯТЃК
ШчЭМ2ЃЌЙ§PзїGHЁЭABгкGЃЌНЛCDгкHЃЌ
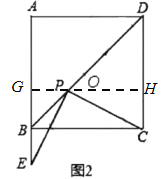
ЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌ
ЁрABЁЮCDЃЌЁЯABDЃН45ЁуЃЌЁЯAЃНЁЯABCЃН90ЁуЃЌ
ЁпGHЁЭABЃЌ
ЁрGHЁЭCDЃЌ
ЁрЁЯEGPЃНЁЯPHCЃН90ЁуЃЌ
ЁрЁЯGEPЃЋЁЯGPEЃН90ЁуЃЌ
ЁпPEЁЭPCЃЌ
ЁрЁЯEPCЃН90ЁуЃЌ
ЁрЁЯGPEЃЋЁЯCPHЃН90ЁуЃЌ
ЁрЁЯGEPЃНЁЯCPHЃЌ
ЁпЁЯABDЃН45ЁуЃЌЁЯEGPЃН90ЁуЃЌ
ЁрЁїBGPЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрBGЃНGPЃЌ
ЁпЁЯEGPЃНЁЯPHCЃНЁЯABCЃН90ЁуЃЌ
ЁрЫФБпаЮBGHCЮЊОиаЮЃЌ
ЁрBGЃНCHЃЌ
ЁрCHЃНGPЃЌ
дкЁїEGPгыЁїPHCжаЃЌ
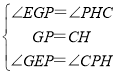
ЁрЁїEGPЁеЁїPHCЃЈAASЃЉЃЌ
ЁрPEЃНPCЃЛ
ЭиеЙгІгУЃКЃЈ1ЃЉШчЭМЃЌЙ§PзїGHЁЭABгкGЃЌНЛCDгкHЃЌ
гЩЬтвтПЩжЊЁїEGPЁеЁїPHCЃЌ
дђEGЃНPHЃЌ
ЁпЁЯAGPЃНЁЯPHDЃНЁЯADCЃН90ЁуЃЌ
ЁрЫФБпаЮAGHDЮЊОиаЮЃЌ
ЁрAGЃНDHЃЌ
ЁпЁЯBDCЃН45ЁуЃЌЁЯPHDЃН90ЁуЃЌ
ЁрЁїPHDЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрDHЃНPHЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпDCЃНABЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпABЁЮCDЃЌ
ЁрЁїDFPЁзЁїBAPЃЌ
Ёр![]() ЃЌ
ЃЌ
гжЁпGHЃНADЃН9ЃЌ
ЁрPHЃН![]() ЃЌPGЃН
ЃЌPGЃН![]() ЃЌ
ЃЌ
ЁрEGЃНDHЃНPHЃН![]() ЃЌ
ЃЌ
ЁрAGЃНDHЃН![]() ЃЌ
ЃЌ
ЁрAEЃНAGЃЋGEЃН![]() ЃЌ
ЃЌ
ЁрSЁїAPEЃН![]() ЃЌ
ЃЌ
ЙЪЁїAPEЕФУцЛ§ЮЊЃК![]() ЃЌ
ЃЌ
ЃЈ2ЃЉЩшPHЃНxЃЌдђPGЃН9ЃxЃЌ
гЩЬтвтПЩжЊЃКAGЃНEGЃНDHЃНPHЃНxЃЌ
дђSЃН![]()
![]()
![]()
![]()
Ёп0ЃМxЃМ9ЃЌ
Ёр0ЃМSЁм![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК0ЃМSЁм![]() ЃЎ
ЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ