题目内容
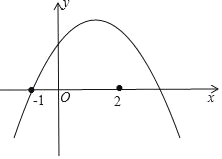
【题目】已知抛物线y=ax2+bx+c(a<0)经过点(﹣1,0),且满足4a+2b+c>0,有下列结论:①a+b>0;②﹣a+b+c>0;③b2﹣2ac>5a2.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3
【答案】D
【解析】
利用题意画出二次函数的大致图象,利用对称轴的位置得到![]() 则可对①进行判断;利用a<0,b>0,c>0可对②进行判断;由a﹣b+c=0,即b=a+c,则4a+2(b+c)+c>0,所以2a+c>0,变形b2﹣2ac﹣5a2=﹣(2a+c)(2a﹣c),则可对③进行判断.
则可对①进行判断;利用a<0,b>0,c>0可对②进行判断;由a﹣b+c=0,即b=a+c,则4a+2(b+c)+c>0,所以2a+c>0,变形b2﹣2ac﹣5a2=﹣(2a+c)(2a﹣c),则可对③进行判断.
解:如图,∵抛物线过点(﹣1,0),且满足4a+2b+c>0,
∴抛物线的对称轴![]()
∴b>﹣a,即a+b>0,所以①正确;
∵a<0,b>0,c>0,
∴﹣a+b+c>0,所以②正确;
∵a﹣b+c=0,即b=a+c,
∴4a+2(b+c)+c>0,
∴2a+c>0,
∴b2﹣2ac﹣5a2=(a+c)2﹣2ac﹣5a2=﹣(2a+c)(2a﹣c),
而2a+c>0,2a﹣c<0,
∴∴b2﹣2ac﹣5a2>0,即b2﹣2ac>5a2.所以③正确.
故选:D.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目