题目内容
【题目】已知四边形ABCD是平行四边形,AD=BD,过点D作DE⊥AB于点E,过点A作AH⊥BD于点H,交DE、BC分别于点F、G,连接CF.

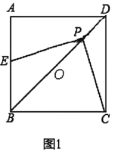
(1)如图1,求证:∠BAG=∠FCB;
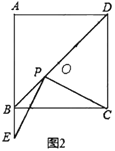
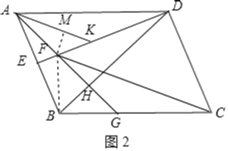
(2)如图2,过点A作AK平分∠DAF交ED于点K,若AK=1,∠FCD=45°,求DF的长;
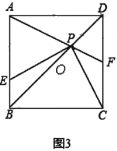
(3)如图3,若AD=10,DH=6,求CF的长.
【答案】(1)见解析;(2)DF=![]() ;(3)CF=
;(3)CF=![]() .
.
【解析】
(1)本题连接BF.设∠BAG=x,∠DAG=y,由∠BDE+∠DFH=90°,∠BAG+∠AFE=90°,∠DFH=∠AFE(对顶角相等)得∠BDE=∠BAG.再通过角之间的关系,证明∠FDC+∠FBC=180°从而得到点F、B、C、D四点共圆,所以∠FCB=∠BDE=x,可证明∠BAG=∠FCB.
(2)本题主要根据平行四边形的性质得出∠BAD=∠BCD,又由(1)∠BAG=∠FCB,得∠DAF=∠FCD=45°,因为AH⊥BD进而得到∠ADH=45°,这样又因为∠FAK=∠DAK=22.5°,∠ADE=∠BDE=22.5°,这样就可以利用角之间的关系找到线段之间的关系,求出DF的长.
(3)连接BF,本题主要利用勾股定理求出AH、FH的长,再在Rt△AHB和Rt△FHD中,分别表示出AB2和DF2,这样就可以在Rt△FDC中,利用勾股定理,求出CF的长度.
(1)如图1,连接BF.
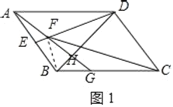
设∠BAG=x,∠DAG=y
∵AD=BD,DE⊥AB于点E
∴直线DE是等腰三角形的对称轴
∴∠ABF=∠BAG=x,∠DBF=∠DAG=y,∠ADE=∠BDE
∴∠ABD=∠BAD=∠BAG+∠DAG=x+y
∵AH⊥BD于点H
∴∠AHD=90°∴∠BDE+∠DFH=90°
∵∠BAG+∠AFE=90°,∠DFH=∠AFE(对顶角相等)
∴∠BDE=∠BAG=x
∴∠ADE=∠BDE=x,∠ADB=∠ADE+∠BDE=2x
∵ABCD
∴AD∥BC,AB∥CD
∴∠DBC=∠ADB=2x,∠CDB=∠ABD=x+y
∴∠FDC=∠BDE+∠CDB=x+x+y=2x+y,∠FBC=∠DBF+∠DBC=y+2x
∴∠FDC+∠FBC=4x+2y
∵AB∥CD
∴∠BAD+∠ADC=180°
∵∠BAD=∠BAG+∠DAG=x+y,∠ADC=∠ADB+∠CDB=2x+x+y=3x+y
∴x+y+3x+y=180°
∴4x+2y=180°
∴∠FDC+∠FBC=4x+2y=180°
∴点F、B、C、D四点共圆
∴∠FCB=∠BDE=x
∴∠BAG=∠FCB
(2)如图2,连接BF,作FM⊥AK于点M.
∵四边形ABCD是平行四边形
∴∠BAD=∠BCD
由(1)知,∠BAG=∠FCB
∴∠DAF=∠FCD=45°
∵AH⊥BD
∴∠ADH=45°
由(1)知,∠ADE=∠BDE
∴∠ADE=∠BDE=22.5°
∵AK
∴∠DAK=∠FAK=![]() ∠DAF=22.5°
∠DAF=22.5°
∴∠DAK=∠ADE
∴DK=AK=1
∵∠AKE=∠DAK+∠ADE=45°,DE⊥AB
∴AE=EK=![]() AK=
AK=![]() ,∠EAK=45°
,∠EAK=45°
∴∠BAG=∠EAK﹣∠FAK=22.5°
∴∠BAG=∠FAK
∵FM⊥AK,FE⊥AB
∴FE=FM
在Rt△FMK中,∠FMK=90°,∠AKE=45°
∴FK=![]() FM=
FM=![]() FE
FE
∵FE+FK=EK
∴FE+![]() FE=
FE=![]()
∴FE=![]()
∴FK=![]() ﹣1
﹣1
∴DF=FK+DK=![]()
(3)如图3,连接BF.
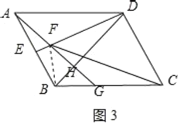
∵AH⊥BD,AD=10,DH=6
∴根据勾股定理得,AH=8
∵BD=AD=10
∴BH=BD﹣DH=4
由(1)知,BF=AF,设FH=a,则BF=AF=8﹣a
由勾股定理得42+a2=(8﹣a)2
∴a=3
∴在Rt△FHD中,∠FHD=90°
由勾股定理得DF2=FH2+DH2=32+62=45
在Rt△AHB中,∠AHB=90°
由勾股定理得AB2=AH2+BH2=82+42=80
∵四边形ABCD是平行四边形
∴AB=CD,AB∥CD
∴∠FDC=∠AED
∵DE⊥AB
∴∠AED=90°
∴∠FDC=90°
∴在R△FDC中,根据勾股定理得CF2=CD2+DF2=AB2+DF2=80+45=125,
∴CF=![]() .
.