题目内容
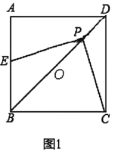
【题目】在下列正多边形中,![]() 是中心,定义:
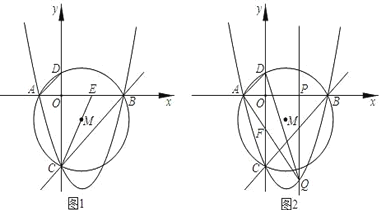
是中心,定义:![]() 为相应正多边形的基本三角形.如图1,
为相应正多边形的基本三角形.如图1,![]() 是正三角形
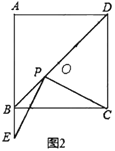
是正三角形![]() 的基本三角形;如图2,
的基本三角形;如图2,![]() 是正方形
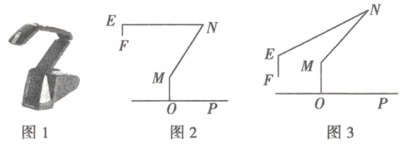
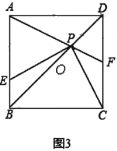
是正方形![]() 的基本三角形;如图3,
的基本三角形;如图3,![]() 为正
为正![]() 边形
边形![]() …的基本三角形.将基本
…的基本三角形.将基本![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 角度得
角度得![]() .
.
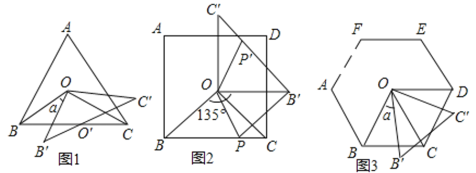
(1)若线段![]() 与线段
与线段![]() 相交点
相交点![]() ,则:
,则:
图1中![]() 的取值范围是________;
的取值范围是________;
图3中![]() 的取值范围是________;
的取值范围是________;
(2)在图1中,求证![]()
(3)在图2中,正方形边长为4,![]() ,边
,边![]() 上的一点
上的一点![]() 旋转后的对应点为
旋转后的对应点为![]() ,若
,若![]() 有最小值时,求出该最小值及此时
有最小值时,求出该最小值及此时![]() 的长度;
的长度;
(4)如图3,当![]() 时,直接写出
时,直接写出![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)见解析;(3)最小值:
;(2)见解析;(3)最小值:![]() ,此时
,此时![]() =2+
=2+![]() ;(4)
;(4)![]()
【解析】
(1)根据正多边形的中心角的定义即可解决问题;
(2)如图1中,作OE⊥BC于E,OF⊥![]() 于F,连接
于F,连接![]() .利用全等三角形的性质分别证明:BE=
.利用全等三角形的性质分别证明:BE=![]() ,
,![]() 即可解决问题;
即可解决问题;
(3)如图2中,作点O关于BC的对称点E,连接OE交BC于K,连接![]() 交BC于点
交BC于点![]() ,连接
,连接![]() ,此时
,此时![]() 的值最小,即
的值最小,即![]() 有最小值.
有最小值.
(4)利用等腰三角形三线合一的性质即可解决问题;
(1)由题意图1中,∵△ABC是等边三角形,O是中心,
∴∠AOB=120°
∴∠α的取值范围是:0°<α≤120°,
图3中,∵ABCDEF…是正n边形,O是中心,
∴∠BOC=![]() ,
,
∴∠α的取值范围是:0°<α≤![]() ,
,
故答案为:0°<α≤120°,0°<α≤![]() .
.
(2)如图1中,作OE⊥BC于E,OF⊥![]() 于F,连接
于F,连接![]() .
.

∵∠OEB=∠OF![]() =90°,
=90°,
根据题意,O是中心,∴OB=OC,
∴∠OBE=∠![]() ,
,
∴△OBE≌△O![]() F(AAS),
F(AAS),
∴OE=OF,BE=![]() F
F
∵![]() ,
,
∴Rt△![]() ≌Rt△
≌Rt△![]() (HL),
(HL),
∴![]() ,
,
∴![]() .
.
(3)如图2中,作点O关于BC的对称点E,连接OE交BC于K,连接![]() 交BC于点
交BC于点![]() ,连接
,连接![]() ,此时
,此时![]() 的值最小.
的值最小.
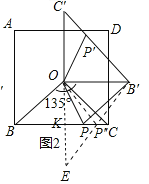
∵∠![]() =135°,∠BOC=90°,
=135°,∠BOC=90°,
∴∠OCB=∠![]() =45°,
=45°,
∴![]() ∥BC,
∥BC,
∵OK⊥BC,OB=OC,
∴BK=CK=2,OB=2![]() ,
,
∵![]() ∥
∥![]() ,OK=KE,
,OK=KE,
∴![]() ,
,
∴![]() =
=![]()
![]() =
=![]() ,
,
∴![]() =2+
=2+![]() ,
,
在Rt△![]() 中,
中,![]() =
=![]() .
.
∵![]() ,
,
∴![]() 有最小值,最小值为
有最小值,最小值为![]() ,此时
,此时![]() =2+
=2+![]() .
.
(4)如图3中,
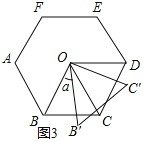
∵ABCDEF…是正n边形,O是中心,
∴∠BOC=![]() ,
,
∵OC⊥![]() ,
, ![]() ,
,
∴∠![]() =
=![]() ∠
∠![]() =
=![]() ∠BOC=
∠BOC=![]() ,
,
∴α=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案