题目内容
已知抛物线 (m是常数,
(m是常数,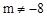 )与x轴有两个不同的交点A、B,点A、点B关于直线x=1对称,抛物线的顶点为C.
)与x轴有两个不同的交点A、B,点A、点B关于直线x=1对称,抛物线的顶点为C.
(1)此抛物线的解析式;
(2)求点A、B、C的坐标.
(1)y=x2-2x;(2)(0,0),(2,0),(1,-1).
解析试题分析:(1)根据已知条件知,该抛物线的对称轴是x=1,然后利用抛物线对称轴方程列出关于m的方程 ,则易求m的值;
,则易求m的值;
(2)根据(1)中的函数解析式知,分别求当x=0,y的值;当y=0时,x的值.
试题解析::(1)∵抛物线 (m为常数,m≠-8))的对称轴为
(m为常数,m≠-8))的对称轴为 ,而抛物线与x轴有两个不同的交点A、B,点A、点B关于直线x=1对称,
,而抛物线与x轴有两个不同的交点A、B,点A、点B关于直线x=1对称,
∴ ,解得m=-6.
,解得m=-6.
∴所求抛物经的解析式为y=x2-2x.
(2)当y=0时,x2-2x=0,解得x1=0,x2=2.
又y=x2-2x=(x-1)2-1,
∴点A、B、C的坐标.分别为(0,0),(2,0),(1,-1).
考点:1.二次函数的性质;2.抛物线与x轴的交点.

练习册系列答案
相关题目
已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表:
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 8 | 3 | 0 | -1 | 0 | 3 | … |
(2)当x为何值时,y有最小值,最小值是多少?
(3)若A(m,y1),B(m+2,y2)两点都在该函数的图象上,计算当m 取何值时,
 ?
?  x+150,成本为20元/件,月利润为W内(元);②若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
x+150,成本为20元/件,月利润为W内(元);②若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳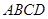 中,
中,  , 高
, 高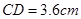 (如图1). 动点
(如图1). 动点 同时从点
同时从点 出发, 点
出发, 点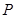 沿
沿 运动到点
运动到点 停止, 点
停止, 点 沿
沿 运动到点
运动到点 时,点
时,点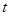 (s)时,
(s)时,  的面积为
的面积为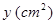 (如图2). 分别以
(如图2). 分别以 为横、纵坐标建立直角坐标系, 已知点
为横、纵坐标建立直角坐标系, 已知点 边上从
边上从 运动时,
运动时,  与
与 .
.

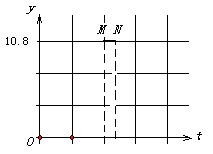
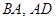 的长度;
的长度; 边上和
边上和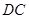 边上运动时,
边上运动时, 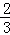 ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
 经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍.
经过点A和点C,动点P在x轴上以每秒1个长度单位的速度由抛物线与x轴的另一个交点B向点A运动,点Q由点C沿线段CA向点A运动且速度是点P运动速度的2倍.
 .
.
 的解集.
的解集.