题目内容
已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表:
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 8 | 3 | 0 | -1 | 0 | 3 | … |
(2)当x为何值时,y有最小值,最小值是多少?
(3)若A(m,y1),B(m+2,y2)两点都在该函数的图象上,计算当m 取何值时,
 ?
?
(1)y=x2-4x+3;(2)当x=2时,ymin=-1;(3)m<1.
解析试题分析:(1)由表格得到二次函数与x轴的两交点坐标,设出二次函数的两根式方程,将(0,3)代入求出a的值,即可确定出二次函数解析式;
(2)将(1)得出的函数解析式配方后,根据完全平方式大于等于0,即可求出y的最小值,以及此时x的值;
(3)将A点坐标代入二次函数解析式中表示出y1,B坐标代入表示出y2,由y1>y2列出关于m的不等式,求出不等式的解集即可得到m的范围.
试题解析:(1)由表格得:二次函数与x轴的两交点分别为(1,0),(3,0),
设二次函数解析式为y=a(x-1)(x-3),
将x=0,y=3代入得:3=3a,即a=1,
则二次函数解析式为y=(x-1)(x-3)=x2-4x+3.
(2)由(1)y=x2-4x+3=(x-2)2-1,
则当x=2时,ymin=-1.
将A坐标代入二次函数解析式得:y1=m2-4m+3;
B坐标代入二次函数解析式得:y2=(m+2)2-4(m+2)+3=m2-1,
若y1>y2,则m2-4m+3>m2-1,
解得:m<1.
考点:1.待定系数法求二次函数解析式;2.二次函数图象上点的坐标特征;3.二次函数的最值.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
已知抛物线y=x²-4x+3.
(1)该抛物线的对称轴是 ,顶点坐标 ;
(2)将该抛物线向上平移2个单位长度,再向左平移3个单位长度得到新的二次函数图像,请写出相应的解析式,并用列表,描点,连线的方法画出新二次函数的图像;
| x | … | | | | | | … |
| y | … | | | | | | … |

(3)新图像上两点A(x1,y1),B(x2,y2),它们的横坐标满足<-2,且-1<<0,试比较y1,y2,0三者的大小关系.
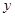 轴于点
轴于点 ,交
,交 轴于
轴于 ,
, 两点(点
两点(点
 的垂线交抛物线于点
的垂线交抛物线于点 ,如果以点
,如果以点 相切,先补全图形,再判断直线
相切,先补全图形,再判断直线 与⊙
与⊙ 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于 的面积最大?求出
的面积最大?求出 (k为正整数).
(k为正整数).
 (k为正整数)有两个不相等的整数解,点A(m,y1),B(m+1,y2),C(m+2,y3)都在二次函数
(k为正整数)有两个不相等的整数解,点A(m,y1),B(m+1,y2),C(m+2,y3)都在二次函数 (m是常数,
(m是常数,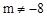 )与x轴有两个不同的交点A、B,点A、点B关于直线x=1对称,抛物线的顶点为C.
)与x轴有两个不同的交点A、B,点A、点B关于直线x=1对称,抛物线的顶点为C.
 米,面积为
米,面积为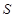 平方米.(注:
平方米.(注: 的近似值取3)
的近似值取3)