题目内容
某商店进了一批服装,每件成本50元,如果按每件60元出售,可销售800件,如果每件提价5元出售,其销量将减少100件。
(1)求售价为70元时的销售量及销售利润;
(2)求销售利润y(元)与售价x(元)之间的函数关系,并求售价为多少元时获得最大利润;
(3)如果商店销售这批服装想获利12000元,那么这批服装的定价是多少元?
(1)600,12000;(2)y=-20(x-75)2+12500,75;(3)70元或80元.
解析试题分析:此题应明确公式:销售利润=销售量×(售价-成本),求售价为多少元时获得最大利润,需考虑二次函数最值问题.
试题解析:(1)销售量为800-20×(70-60)=600(件),
600×(70-50)=600×20=12000(元)
(2)y=(x-50)[800-20(x-60)]=-20x2+3000x-100000,
=-20(x-75)2+12500,
所以当销售价为75元时获得最大利润为12500元.
(3)当y=12000时,
-20(x-75)2+12500=12000,
解得x1=70,x2=80,
即定价为70元或80元时这批服装可获利12000元.
考点: 二次函数的应用.

练习册系列答案
相关题目
 x2+
x2+ x(0≤x≤10).发射3 s后,导弹到达A点,此时位于与L同一水面的R处雷达站测得AR的距离是2 km,再过3 s后,导弹到达B点.
x(0≤x≤10).发射3 s后,导弹到达A点,此时位于与L同一水面的R处雷达站测得AR的距离是2 km,再过3 s后,导弹到达B点.


 ,若存在,求出P点坐标;若不存在,请说明理由.
,若存在,求出P点坐标;若不存在,请说明理由. 中,矩形OABC过原点O,且A(0,2)、C(6,0),∠AOC的平分线交AB于点D.
中,矩形OABC过原点O,且A(0,2)、C(6,0),∠AOC的平分线交AB于点D. 个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿
个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿 轴正方向移动.设移动时间为
轴正方向移动.设移动时间为 秒.
秒.
 (x-t)2+t(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
(x-t)2+t(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由. (m是常数,
(m是常数,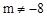 )与x轴有两个不同的交点A、B,点A、点B关于直线x=1对称,抛物线的顶点为C.
)与x轴有两个不同的交点A、B,点A、点B关于直线x=1对称,抛物线的顶点为C.