题目内容
如图,某中学校园有一块长为35m,宽为16m的长方形空地,其中有一面已经铺设长为26m的篱笆围墙,学校设计在这片空地上,利用这面围墙和用尽已有的可制作50m长的篱笆材料,围成一个矩形花园或围成一个半圆花园,请回答以下问题:
(1)能否围成面积为300m2的矩形花园?若能,请写出其中一种设计方案,若不能,请说明理由.
(2)若围成一个半圆花园,则该如何设计?请写出你的设计方案.(π取3.14)
(3)围成的各种设计中,最大面积是多少?
(1)能,设计方案见解析;(2)设计方案见解析;(3)343.43m2.
解析试题分析:(1)首先表示出矩形的长与宽,利用矩形面积得出等式,进而解方程得出;
(2)利用已知得出设新增加am,则半圆弧长为: ,进而得出a的值,即可得出答案;
,进而得出a的值,即可得出答案;
(3)利用二次函数最值求法得出矩形最值再利用半圆面积公式得出半圆面积,进而比较即可.
试题解析:(1)设垂直于已经铺设长为26m的篱笆围墙的一边为xm,则平行于原篱笆的长为(50-2x)m,
根据题意得出:x(50-2x)=300,
解得:x1=10,x2=15,
当x=10,则50-20=30>26,故不合题意舍去,
∴能围成面积为300m2的矩形花园,此时长为20m,宽为15m;
(2)∵当r=13时,∴l半圆=πr=3.14×13=40.82<50,
∴半圆的直径应大于26m,设新增加am,则半圆弧长为: ,
,
∴a+ =50,
=50,
解得:a≈3.57,
∴半圆直径为:26+3.57=29.57(m),
∴半圆的半径为:14.79m;
(3)S1=x(50-2x)=-2x2+50x,
当x=12.5时,S最大= =312.5(m2),
=312.5(m2),
S半圆= π×14.792≈343.43(m2),
π×14.792≈343.43(m2),
∴围成的各种设计中,最大面积是半圆面积为343.43m2.
考点: 1.二次函数的应用;2.一元二次方程的应用.

 中,矩形OABC过原点O,且A(0,2)、C(6,0),∠AOC的平分线交AB于点D.
中,矩形OABC过原点O,且A(0,2)、C(6,0),∠AOC的平分线交AB于点D. 个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿
个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿 轴正方向移动.设移动时间为
轴正方向移动.设移动时间为 秒.
秒.
 (x-t)2+t(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
(x-t)2+t(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由. 分别与y轴、x轴相交于A、B两点,与二次函数
分别与y轴、x轴相交于A、B两点,与二次函数 的图像交于A、C两点.
的图像交于A、C两点.
 ,
,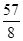 )时,求直线AB的解析式;
)时,求直线AB的解析式;  (m是常数,
(m是常数,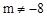 )与x轴有两个不同的交点A、B,点A、点B关于直线x=1对称,抛物线的顶点为C.
)与x轴有两个不同的交点A、B,点A、点B关于直线x=1对称,抛物线的顶点为C. 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C(0,4),D为OC的中点.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C(0,4),D为OC的中点.
 ?若存在,求出点G的坐标;若不存在请说明理由.
?若存在,求出点G的坐标;若不存在请说明理由. 的图象与x轴交于点A(-1, 0),与y轴交于点C(0,-5),且经过点D(3,-8).
的图象与x轴交于点A(-1, 0),与y轴交于点C(0,-5),且经过点D(3,-8).
 的坐标.
的坐标. 为边长是
为边长是 的等边三角形,四边形
的等边三角形,四边形 为边长是6的正方形. 现将等边
为边长是6的正方形. 现将等边 与点
与点 重合,点
重合,点 、
、 、
、 在同一条直线上,
在同一条直线上, 方向向右匀速运动,当点
方向向右匀速运动,当点 秒(
秒( ).
).
 ,请直接写出
,请直接写出 与点
与点 重合时,作
重合时,作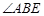 的角平分线
的角平分线 交
交 于点
于点 ,将
,将 绕点
绕点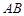 与边
与边 重合,得到
重合,得到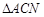 . 在线段
. 在线段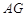 上是否存在
上是否存在 点,使得
点,使得 为等腰三角形. 如果存在,求线段
为等腰三角形. 如果存在,求线段 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由. 个单位长度,其余条件保持不变.
个单位长度,其余条件保持不变.  点从
点从 以每秒
以每秒 个单位长度开始移动,
个单位长度开始移动, 交折线
交折线 于
于 点,则当
点,则当 时,求
时,求