题目内容
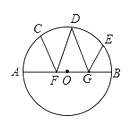
【题目】如图,在⊙O中,F,G是直径AB上的两点,C,D,E是半圆上的三点,如果弧AC的度数为60°,弧BE的度数为20°,∠CFA=∠DFB,∠DGA=∠EGB.求∠FDG的大小.
【答案】50°.
【解析】
作C关于AB的对称点M,作E关于AB的对称点N,连接CM,FM,求出∠AFM=∠BFD,推出D、F、M三点共线,D、G、N三点共线,求出弧AM=60°,弧BN=20°,即可求出答案.
如图:作点C关于AB的对称点M,点E关于AB的对称点N,连结CM、FM,设CM交AB于点Q,

依题可得AB⊥CM,CQ=MQ,
∴∠CFA=∠AFM,
又∵∠CFA=∠DFB,
∴∠AFM=∠DFB,
∴D、F、M三点共线,
同理可得D、G、N三点共线,
又∵弧AC=60°,弧BE=20°,
∴弧AM=弧AC=60°,弧BN=弧BE=20°,
∴弧MN=180°-60°-20°=100°,
∴∠FDG=![]() ×100°=50°.
×100°=50°.

练习册系列答案
相关题目
【题目】甲、乙两台机床同时加工直径为![]() 的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取
的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取![]() 件进行检测,结果如下(单位:
件进行检测,结果如下(单位:![]() ):
):
甲 |
|
|
|
|
|
乙 |
|
|
|
|
|
(1)分别求出这两台机床所加工零件直径的平均数和方差;
(2)根据所学的统计知识,你认为哪一台机床生产零件的稳定性更好一些,说明理由.