题目内容
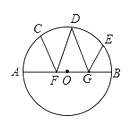
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,垂足为
,垂足为![]() ,点
,点![]() 是边
是边![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 交线段
交线段![]() 于点
于点![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,交线段
,交线段![]() 于点
于点![]() ,设
,设![]() .
.

(1)用含![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
(2)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出定义域;
之间的函数关系式,并写出定义域;
(3)若![]() 为直角三角形,求出
为直角三角形,求出![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据题意可得△ABC和△BPF为等边三角形,由![]() 及等边三角形的性质得出PF=GF=x,从而表示出DG=BF+FG-BD=2x-1;
及等边三角形的性质得出PF=GF=x,从而表示出DG=BF+FG-BD=2x-1;
(2)由含30°直角三角形的性质表示出DE,由(1)可表示出DF,再根据三角形面积的计算公式即可解答;
(3)若![]() 为直角三角形,则∠PFE=90°或∠PEF=90°,根据直角三角形的性质列出方程求解即可.
为直角三角形,则∠PFE=90°或∠PEF=90°,根据直角三角形的性质列出方程求解即可.
解:(1)∵在![]() 中,
中,![]()
∴△ABC为等边三角形,
∴∠BAC=∠ABC=∠ACB=60°,
∵![]()
∴∠BPF=∠BAC=∠BFP=60°,
∴△BPF为等边三角形,
∴BF=BP=PF=x,∠PFC=120°,
∵![]()
∴∠BPE=90°,
∴∠FPE=30°,
∴∠FGP=30°,
∴PF=GF=x
又∵AD⊥BC,
∴BD=CD=1,
∴DG=BF+FG-BD=2x-1
故![]()
(2)由(1)可知DF=BD-BF=1-x,
∵∠FGP=30°,∠ADG=90°,
∴EG=2DE
由勾股定理得:![]() ,
,
∴![]()
∴![]() ,
,
∴![]()
∵![]() ,解得
,解得![]() ,
,
∴定义域为:![]()
(3)∵∠FPG=30°,
∴若![]() 为直角三角形,则∠PFE=90°或∠PEF=90°,
为直角三角形,则∠PFE=90°或∠PEF=90°,
①当∠PFE=90°时,
∠EFD=120°-90°=30°,
∴△EFG为等腰三角形,
∴DF=DG
∵DF=1-x,DG=2x-1,
∴1-x =2x-1
解得:![]()
②当∠PEF=90°时,
∠FED=90°-60°=30°,
∴DE=![]() ,
,
∵![]() ,DF=1-x,
,DF=1-x,
∴![]() ,
,
解得:![]()
综上所述,![]() 的长为
的长为![]() 或
或![]() .
.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目