题目内容
【题目】为保障国庆70周年南口阅兵训练基地全体人员的生活，需通过铁路、公路两种运输方式运送生活物资．原计划铁路运输物资的5倍是公路运输的8倍，实际铁路运输的物资减少了15吨，公路运输增加了15吨，且铁路运输物资的2倍比公路运输的3倍少60吨．
（1）原计划铁路、公路分别运输多少吨物资到训练基地？
（2）现采用微型集装箱装载这些物资，每个集装箱装满后箱货总重量为1.6吨，空箱重量为0.1吨．为增加集装箱的载货量将其进行改造，改造后每个集装箱装满后箱货总重量比改造前增加
吨，空箱重量比改造前减少
吨，其中
．改造前的集装箱每个装满后恰好装下这些物资．若用改造后的集装箱来装载这些物资，改造后的集装箱个数比改造前少用10个．设改造后的集装箱最大载货量总重量为
吨，求关于的函数关系式以及的最大值．
【答案】（1）原计划铁路、公路分别运输120吨，75吨物资到训练基地；（2）w＝132m＋180，w最大值为232.8吨．
【解析】
（1）设原计划铁路、公路分别运输a吨，b吨物资到训练基地，根据“原计划铁路运输物资的5倍是公路运输的8倍，实际铁路运输的物资减少了15吨，公路运输增加了15吨，且铁路运输物资的2倍比公路运输的3倍少60吨”列出方程组，求解即可；
（2）首先求出改造前的集装箱的个数，然后列出w关于m的函数关系式，利用一次函数的性质求解．
解：（1）设原计划铁路、公路分别运输a吨，b吨物资到训练基地，
由题意得：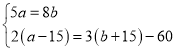
，
解得：
，
答：原计划铁路、公路分别运输120吨，75吨物资到训练基地；
（2）改造前的集装箱的个数为：
＝130个，
由题意可得：w＝（13010）[（1.6＋m）（0.1
）]＝132m＋180，
∴w随m的增大而增大，
∵0.1≤m≤0.4．
∴当m＝0.4时，w最大值＝232.8吨．
