题目内容
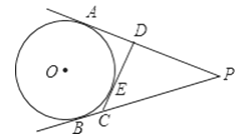
【题目】如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,分别交PA、PB于点C、D.若PA、PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根,求△PCD的周长.
【答案】2
【解析】
由PA、PB切⊙O于A、B两点,CD切⊙O于点E,根据切线长定理,可得PA=PB,又由PA、PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根,根据根与系数的关系,可求得PA与PB的长,又由CD切⊙0于点E,即可得△PCD的周长等于PA+PB.
解:∵PA、PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根,
∴PA+PB=m,PAPB=m﹣1,
∵PA、PB切⊙O于A、B两点,
∴PA=PB=![]() ,
,
即![]()
![]() =m﹣1,
=m﹣1,
即m2﹣4m+4=0,
解得:m=2,
∴PA=PB=1,
∵PA、PB切⊙O于A、B两点,CD切⊙O于点E,
∴AD=ED,BC=EC,
∴△PCD的周长为:PD+CD+PC=PD+DE+EC+PC=PD+AD+BC+PC=PA+PB=2.

练习册系列答案
相关题目