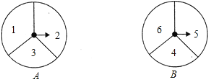题目内容
【题目】如图,E,F分别是矩形ABCD的边AB,AD上的点,∠FEC=∠FCE=45°.
(1)求证:AF=CD.
(2)若AD=3,△EFC的面积为4,求线段BE的长.

【答案】(1)详见解析.(2)![]() .
.
【解析】
(1)由AAS证明△AEF≌△DFC,即可得出结论;
(2)由△EFC的面积求出EF=CF,由勾股定理求出EC,再由勾股定理求出BE即可.
(1)证明:∵在△CEF中,∠FEC=∠FCE=45°,
∴FE=FC,∠EFC=90°,
∴∠AFE+∠CFD=90°,
又∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴∠CFD+∠DCF=90°,
∴∠AFE=∠DCF,
在△AEF和△DFC中,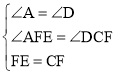 ,
,
∴△AEF≌△DFC(AAS)
∴AF=CD;
(2)解:由(1)得△CEF中,∠EFC=90°,FE=FC,△EFC的面积为4
∴![]()
∴![]() ,
,
在Rt△CEF中,![]() ,
,
又∵四边形ABCD是矩形,∴∠B=90°,AD=BC=3
∴在Rt△BEC中,BE2=CE2﹣BC2=16﹣32=7,
∴![]() .
.

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案【题目】小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折(折扣相同),其余两次均按标价购买.三次购买商品A、B的数量和费用如下表:
购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
(1)小林以折扣价购买商品A、B是第 次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
【题目】有两个可以自由转动的质地均匀转盘![]() 、
、![]() 都被分成了
都被分成了![]() 个全等的扇形,在每一扇形内均标有不同的自然数,如图所示.转动转盘
个全等的扇形,在每一扇形内均标有不同的自然数,如图所示.转动转盘![]() 、
、![]() ,两个转盘停止后观察两个指针所指扇形内的数字(若指针停在扇形的边线上,当作指向下方的扇形).
,两个转盘停止后观察两个指针所指扇形内的数字(若指针停在扇形的边线上,当作指向下方的扇形).
(1)小明同学转动转盘![]() ,小华同学转动转盘
,小华同学转动转盘![]() ,他们都转了
,他们都转了![]() 次,结果如下:
次,结果如下:
指针停靠的扇形内的数字 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
![]() 求出表中
求出表中![]() 的值.
的值.
![]() 计算
计算![]() 盘中“指针停靠的扇形内的数字为
盘中“指针停靠的扇形内的数字为![]() ”的频率;
”的频率;
(2)小明转动![]() 盘一次,指针停靠的扇形内的数字作为十位数字,小华转动
盘一次,指针停靠的扇形内的数字作为十位数字,小华转动![]() 盘一次,指针停靠的扇形内的数字作为个位数字,用列表或画树状图的方法求出“所得的两位数为
盘一次,指针停靠的扇形内的数字作为个位数字,用列表或画树状图的方法求出“所得的两位数为![]() 的倍数”(记为事件
的倍数”(记为事件![]() )的概率.
)的概率.