题目内容
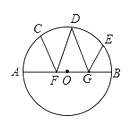
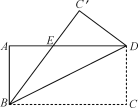
【题目】如图,将矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于点E,CD=6,BC=8,则DE的长度为________.
【答案】![]()
【解析】
先根据折叠的性质得到∠DBC=∠DBE,再由AD∥BC得到∠DBC=∠BDE,则∠DBE=∠BDE,于是可判断BE=DE设AE=x,则DE=BE=8x,然后在Rt△ABE中利用勾股定理得到x2+62=(8x)2,再解方程即可求出AE,再得到DE的长.
∵△BDC′是由△BDC折叠得到,
∴∠DBC=∠DBE,
∵AD∥BC,
∴∠DBC=∠BDE,
∴∠DBE=∠BDE,
∴BE=DE
设AE=x,则DE=ADAE=BC-x=8x,BE=8x,
在Rt△ABE中,∵AE2+AB2=BE2,
∴x2+62=(8x)2,解得x=![]() ,
,
即AE=![]()
∴DE=AD-AE=8-![]() =
=![]()
故答案为:![]() .
.

练习册系列答案
相关题目