题目内容
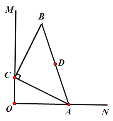
【题目】如图,∠MON =∠ACB = 90°,AC = BC,AB =5,△ABC顶点A、C分别在ON、OM上,点D是AB边上的中点,当点A在边ON上运动时,点C随之在边OM上运动,则OD的最大值为_____.
【答案】![]() .
.
【解析】
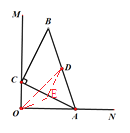
如图,取AC的中点E,连接OE、DE、OD,由OD≤OE+DE,可得当O、D、E三点共线时,点D到点O的距离最大,再根据已知条件,结合三角形的中位线定理及直角三角形斜边中线的性质即可求得OD的最大值.
如图,取AC的中点E,连接OE、DE、OD,
∵OD≤OE+DE,
∴当O、D、E三点共线时,点D到点O的距离最大,
∵∠ACB = 90°,AC = BC,AB =5,
∴AC=BC=![]()
∵点E为AC的中点,点D为AB的中点,
∴DE为△ABC的中位线,
∴DE=![]() BC=
BC=![]() ;
;
在Rt△ABC中,点E为AC的中点,
∴OE=![]() AC=
AC=![]() ;
;
∴OD的最大值为:OD+OE=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目