��Ŀ����
����Ŀ��ij��������һ����Ʒ���ɱ�ÿǧ��40Ԫ���涨ÿǧ���ۼ۲����ڳɱ����Ҳ�����80Ԫ�����г����飬ÿ���������y��ǧ�ˣ���ÿǧ���ۼ�x��Ԫ������һ�κ�����ϵ�������������±���
�ۼ�x��Ԫ/ǧ�ˣ� | 50 | 60 | 70 |
������y��ǧ�ˣ� | 100 | 80 | 60 |
��1����y��x֮��ĺ�������ʽ��
��2������Ʒÿ���������ΪW��Ԫ�������ۼ�x��Ϊ����Ԫʱ������ÿ���ܻ�����������������Ƕ��٣�
��3���������Ҫ���ÿ�첻����1350Ԫ�������ҷ��ϳ����Լ��Ĺ涨����ô����Ʒÿǧ���ۼ۵�ȡֵ��Χ�Ƕ��٣���˵�����ɣ�
���𰸡���1��y����2x+200 ��40��x��80������2���ۼ�Ϊ70Ԫʱ�������������������1800Ԫ����3��55��x��80�����ɼ�����
��������
��1������ϵ�������ɵã�
��2��������������ÿǧ�����������������ɵú�������ʽ�������䷽�ɶ���ʽ���ɵ���ֵ�����
��3�����W��1350ʱx��ֵ���ٸ��ݶ��κ������������W��1350ʱx��ȡֵ��Χ���̶�������ÿǧ���ۼ۲����ڳɱ��Ҳ�����80Ԫ���ó��𰸣�
��1����y��kx+b��
����50��100������60��80�����룬�ã�
![]() ��
��
��ã�![]() ��
��
��y����2x+200 ��40��x��80����
��2��W����x��40������2x+200��
����2x2+280x��8000
����2��x��70��2+1800��
�൱x��70ʱ��Wȡ�����ֵΪ1800��
���ۼ�Ϊ70Ԫʱ�������������������1800Ԫ��
��3����W��1350ʱ���ã���2x2+280x��8000��1350��
��ã�x��55��x��85��
�߸������ߵĿ������£�
���Ե�55��x��85ʱ��W��1350��
�֡�ÿǧ���ۼ۲����ڳɱ����Ҳ�����80Ԫ����40��x��80��
�����Ʒÿǧ���ۼ۵�ȡֵ��Χ��55��x��80��

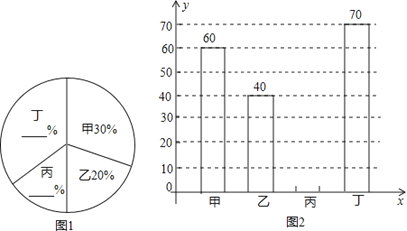
����Ŀ������ijУ��չ�����������й���Ϊ�������Ӱ������Ҫ�����ѧ��ÿ�˽�һ����Ʒ���ֽ�
������ѡ��50��������Ʒ�ijɼ�����λ������ͳ�����£�
�ȼ� | �ɼ�����m��ʾ�� | Ƶ�� | Ƶ�� |
A | 90�� m ��100 | x | 0.08 |
B | 80�� m ��90 | 34 | y |
C | m ��80 | 12 | 0.24 |
�ϼ� |
| 50 | 1 |
������ϱ��ṩ����Ϣ������������⣺
��1������![]() ��ֵΪ_____________��
��ֵΪ_____________��![]() ��ֵΪ______________����ֱ����д�����
��ֵΪ______________����ֱ����д�����
��2�������β�����Ʒ���A�ȼ���ѧ��������A1��A2��A3������ʾ���ָ�У�����ӱ��β�����Ʒ���A�ȼ���ѧ���У������ȡ����ѧ��̸̸���ǵIJ�����ᣬ��ǡ�ó鵽ѧ��A1��A2�ĸ���Ϊ____________����ֱ����д�����