题目内容
【题目】实验探究:
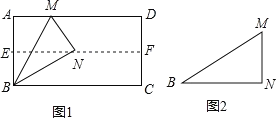
(1)如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论.
(2)将图1中的三角形纸片BMN剪下,如图2,折叠该纸片,探究MN与BM的数量关系,写出折叠方案,并结合方案证明你的结论.
【答案】(1)见解析;(2)见解析.
【解析】
(1)猜想:∠MBN=30°.只要证明△ABN是等边三角形即可;
(2)结论:MN=![]() BM.折纸方案:如图,折叠△BMN,使得点N落在BM上O处,折痕为MP,连接OP.由折叠可知△MOP≌△MNP,只要证明△MOP≌△BOP,即可推出MO=BO=
BM.折纸方案:如图,折叠△BMN,使得点N落在BM上O处,折痕为MP,连接OP.由折叠可知△MOP≌△MNP,只要证明△MOP≌△BOP,即可推出MO=BO=![]() BM;
BM;
(1)猜想:∠MBN=30.
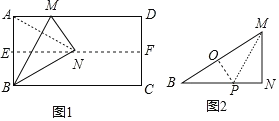
理由:如图1中,连接AN,∵直线EF是AB的垂直平分线,
∴NA=NB,
由折叠可知,BN=AB,
∴AB=BN=AN,
∴△ABN是等边三角形,
∴∠ABN=60,
∴NBM=∠ABM=![]() ∠ABN=30.
∠ABN=30.
(2)结论:MN=![]() BM.
BM.
折纸方案:如图2中,折叠△BMN,使得点N落在BM上O处,折痕为MP,连接OP.
理由:由折叠可知△MOP≌△MNP,
∴MN=OM,∠OMP=∠NMP=![]() ∠OMN=30=∠B,
∠OMN=30=∠B,
∠MOP=∠MNP=90,
∴∠BOP=∠MOP=90,
∵OP=OP,
∴△MOP≌△BOP,
∴MO=BO=![]() BM,
BM,
∴MN=![]() BM.
BM.

练习册系列答案
相关题目