题目内容
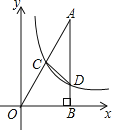
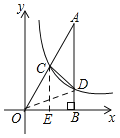
【题目】如图,已知在平面直角坐标系xOy中,Rt△OAB的直角顶点B在x轴的正半轴上,点A在第一象限,反比例函数y=![]() (x>0)的图象经过OA的中点C.交AB于点D,连结CD.若△ACD的面积是2,则k的值是_____.
(x>0)的图象经过OA的中点C.交AB于点D,连结CD.若△ACD的面积是2,则k的值是_____.
【答案】![]()
【解析】
作辅助线,构建直角三角形,利用反比例函数k的几何意义得到S△OCE=S△OBD=![]() k,根据OA的中点C,利用△OCE∽△OAB得到面积比为1:4,代入可得结论.
k,根据OA的中点C,利用△OCE∽△OAB得到面积比为1:4,代入可得结论.
解:连接OD,过C作CE∥AB,交x轴于E,
∵∠ABO=90°,反比例函数y=![]() (x>0)的图象经过OA的中点C,
(x>0)的图象经过OA的中点C,
∴S△COE=S△BOD=![]() ,S△ACD=S△OCD=2,
,S△ACD=S△OCD=2,
∵CE∥AB,
∴△OCE∽△OAB,
∴![]() ,
,
∴4S△OCE=S△OAB,
∴4×![]() k=2+2+
k=2+2+![]() k,
k,
∴k=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】我市实施城乡生活垃圾分类管理,推进生态文明建设为增强学生的环保意识,随机抽取![]() 名学生,对他们的垃圾分类投放情况进行调查,这
名学生,对他们的垃圾分类投放情况进行调查,这![]() 名学生分别标记为
名学生分别标记为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中“√”表示投放正确,“×”表示投放错误,统计情况如下表.
,其中“√”表示投放正确,“×”表示投放错误,统计情况如下表.
学生 垃圾类别 |
|
|
|
|
|
|
|
|
厨余垃圾 | √ | √ | √ | √ | √ | √ | √ | √ |
可回收垃圾 | √ | × | √ | × | × | √ | √ | √ |
有害垃圾 | × | √ | × | √ | √ | × | × | √ |
其他垃圾 | × | √ | √ | × | × | √ | √ | √ |
(1)求![]() 名学生中至少有三类垃圾投放正确的概率;
名学生中至少有三类垃圾投放正确的概率;
(2)为进一步了解垃圾分类投放情况,现从![]() 名学生里“有害垃圾”投放错误的学生中随机抽取两人接受采访,试用标记的字母列举所有可能抽取的结果,并求出刚好抽到
名学生里“有害垃圾”投放错误的学生中随机抽取两人接受采访,试用标记的字母列举所有可能抽取的结果,并求出刚好抽到![]() 、
、![]() 两位学生的概率.
两位学生的概率.