ЬтФПФкШн
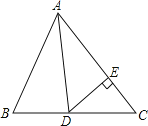
ЁОЬтФПЁПШчЭМЫљЪО,ЁїABCжа,ЁЯB=90ЃЌAB=6cmЃЌBC=8cm.
(1)ЕуPДгЕуAПЊЪМбиABБпЯђBвд1cm/sЕФЫйЖШвЦЖЏ,ЕуQДгBЕуПЊЪМбиBCБпЯђЕуCвд2cm/sЕФЫйЖШвЦЖЏ.ШчЙћP,QЗжБ№ДгA,BЭЌЪБГіЗЂ.

ЂйОЙ§МИУы,ЪЙЁїPBQЕФУцЛ§ЕШгк8![]() ?
?
ЂкЯпЖЮPQФмЗёНЋЁїABCЗжГЩУцЛ§ЯрЕШЕФСНВПЗж?ШєФмЃЌЧѓГідЫЖЏЪБМфЃЛШєВЛФмЫЕУїРэгЩ.
(2)ШєPЕубиЩфЯпABЗНЯђДгAЕуГіЗЂвд1cm/sЕФЫйЖШвЦЖЏЃЌЕуQбиЩфЯпCBЗНЯђДгCЕуГіЗЂвд2cm/sЕФЫйЖШвЦЖЏЃЌPЃЌQЭЌЪБГіЗЂЃЌЮЪМИУыКѓЃЌЁїPBQЕФУцЛ§ЮЊ1![]() ?
?
ЁОД№АИЁПЃЈ1ЃЉОЙ§2УыЛђ4УыЃЌЁїPBQЕФУцЛ§ЕШгк8cm2ЃЛЯпЖЮPQВЛФмЗёНЋЁїABCЗжГЩУцЛ§ЯрЕШЕФСНВПЗжЃЛЃЈ2ЃЉОЙ§ЃЈ![]() ЃЉУыЃЌ5УыЃЌЃЈ
ЃЉУыЃЌ5УыЃЌЃЈ![]() ЃЉУыКѓЃЌЁїPBQЕФУцЛ§ЮЊ1.
ЃЉУыКѓЃЌЁїPBQЕФУцЛ§ЮЊ1.
ЁОНтЮіЁП
ЃЈ1ЃЉЂйОЙ§xУыЃЌЪЙЁїPBQЕФУцЛ§ЕШгк8cm2ЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНСаГіЗНГЬЃЌНтЗНГЬМДПЩЧѓНтЃЛЂкИљОн![]() СаГіЗНГЬЃЌНтЗНГЬМДПЩНтД№ЃЛЃЈ2ЃЉЗжШ§жжЧщПіЃКЂйЕуPдкЯпЖЮABЩЯЃЌЕуQдкЯпЖЮCBЩЯЃЈ0ЃМxЁм4ЃЉЃЛЂкЕуPдкЯпЖЮABЩЯЃЌЕуQдкЯпЖЮCBЕФбгГЄЯпЩЯЃЈ4ЃМxЁм6ЃЉЃЛЂлЕуPдкЩфЯпABЩЯЃЌЕуQдкЩфЯпCBЩЯЃЈxЃО6ЃЉЃЛСаЗНГЬНјааЬжТлЧѓНтМДПЩЃЎ
СаГіЗНГЬЃЌНтЗНГЬМДПЩНтД№ЃЛЃЈ2ЃЉЗжШ§жжЧщПіЃКЂйЕуPдкЯпЖЮABЩЯЃЌЕуQдкЯпЖЮCBЩЯЃЈ0ЃМxЁм4ЃЉЃЛЂкЕуPдкЯпЖЮABЩЯЃЌЕуQдкЯпЖЮCBЕФбгГЄЯпЩЯЃЈ4ЃМxЁм6ЃЉЃЛЂлЕуPдкЩфЯпABЩЯЃЌЕуQдкЩфЯпCBЩЯЃЈxЃО6ЃЉЃЛСаЗНГЬНјааЬжТлЧѓНтМДПЩЃЎ
ЃЈ1ЃЉЂйЩшОЙ§xУыЃЌЪЙЁїPBQЕФУцЛ§ЕШгк8cm2
![]() ЃЈ6-xЃЉ2x=8
ЃЈ6-xЃЉ2x=8
НтЕУx1=2ЃЌx2=4
ЁрОЙ§2УыЛђ4УыЃЌЁїPBQЕФУцЛ§ЕШгк8cm2ЃЛ
Ђк![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
Ёпb2-4ac=36-4ЁС12=-12ЃМ0ЃЌ
ЁрДЫЗНГЬЮоЪЕЪ§ИљЃЌ
ЁрЯпЖЮPQВЛФмЗёНЋЁїABCЗжГЩУцЛ§ЯрЕШЕФСНВПЗжЃЛ
ЃЈ2ЃЉЩшОЙ§xУыЃЌ
ЂйЕБЕуPдкЯпЖЮABЩЯЃЌЕуQдкЯпЖЮCBЩЯЪБЃЌМДЕБ![]() ЪБЃЌ
ЪБЃЌ
![]() ЃЈ6-xЃЉЃЈ8-2xЃЉ=1ЃЌ
ЃЈ6-xЃЉЃЈ8-2xЃЉ=1ЃЌ
x2-10x+23=0ЃЌ
НтЕУ![]() ,
,![]() (Щс)
(Щс)
ЂкЕБЕуPдкЯпЖЮABЩЯЃЌЕуQдкЯпЖЮCBЕФбгГЄЯпЩЯЪБЃЌМДЕБ4ЃМxЁм6ЪБЃЌ
![]() ЃЈ6-xЃЉЃЈ2x-8ЃЉ=1ЃЌ
ЃЈ6-xЃЉЃЈ2x-8ЃЉ=1ЃЌ
x2-10x+25=0ЃЌ
x1=x2=5
ЂлЕБЕуPдкЯпЖЮABЕФбгГЄЯпЩЯЃЌЕуQдкЯпЖЮCBЕФбгГЄЯпЩЯЪБЃЌМДЕБx![]() 6ЪБЃЌ
6ЪБЃЌ
![]() ЃЈx-6ЃЉЃЈ2x-8ЃЉ=1ЃЌ
ЃЈx-6ЃЉЃЈ2x-8ЃЉ=1ЃЌ
x2-10x+23=0ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЈЩсЃЉ
ЃЈЩсЃЉ
злЩЯЫљЪіЃЌОЙ§ЃЈ![]() ЃЉУыЛђ5УыЛђЃЈ
ЃЉУыЛђ5УыЛђЃЈЃЉУыКѓЃЌЁїPBQЕФУцЛ§ЮЊ1.