题目内容
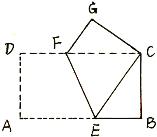
【题目】如图,在平面直角坐标系中,等腰直角三角形 CDE 的腰 CD=2 在 x 轴上,∠ECD=45°,将三角形 CDE 绕点 C 逆时针旋转 75°,点 E 的对应点 N 恰好落在 y 轴上,则点 N 的坐标为( )

A. (0,3) B. (0,2![]() ) C. (0,
) C. (0, ![]() ) D. (0,
) D. (0, ![]() )
)
【答案】C
【解析】
根据旋转得出∠NCE=75°,求出∠NCO,由 CD=2,利用勾股定理求出 CE 的长即为 CN 的长,即 可求出 ON 的长度
∵将三角形 CDE 绕点 C 逆时针旋转 75°,点 E 的对应点 N 恰好落在 OA 上,
∴∠ECN=75°,
∵∠ECD=45°,
∴∠NCO=180°﹣75°﹣45°=60°,
∵AO⊥OB,
∴∠AOB=90°,
∴∠ONC=30°,
∵等腰直角三角形DCE 旋转到△CMN,
∴△CMN 也是等腰直角三角形,
∵CM=2,
∴CN=2![]() ,
,
∴OC=![]()
∴ON=![]()
故选C.

 计算高手系列答案
计算高手系列答案【题目】如图,在△ABC中,∠ACB=90°,∠ABC=25°,O为AB的中点. 将OA绕点O逆时针旋转θ °至OP(0<θ<180),当△BCP恰为轴对称图形时,θ的值为_____________.

【题目】为养成学生课外阅读的习惯,各学校普遍开展了“我的梦.中国梦”课外阅读活动.某校为了解七年级1200名学生课外日阅读所用时间情况,从中随机抽查了部分同学,进行了相关统计,整理并绘制出如下不完整的频数分布表和频数分布直方图,请根据图表信息解答下列问题:
(1)表中 a= ,b= ;
(2)请补全频数分布直方图中空缺的部分;
(3)样本中,学生日阅读所用时间的中位数落在第 组;
(4)请估计该校七年级学生日阅读量不足 1 小时的人数.
组别 | 时间段(小时) | 频数 | 频率 |
1 | 0≤x<0.5 | 10 | 0.05 |
2 | 0.5≤x<1.0 | 20 | 0.10 |
3 | 1.0≤x<1.5 | 80 | b |
4 | 1.5≤x<2.0 | a | 0.35 |
5 | 2.0≤x<2.5 | 12 | 0.06 |
6 | 2.5≤x<3.0 | 8 | 0.04 |