题目内容
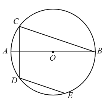
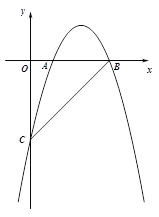
【题目】如图1,在平面直角坐标系内,A,B为x轴上两点,以AB为直径的⊙M交y轴于C,D两点,C为![]() 的中点,弦AE交y轴于点F,且点A的坐标为(﹣2,0),CD=8.
的中点,弦AE交y轴于点F,且点A的坐标为(﹣2,0),CD=8.
(1)求⊙M的半径;
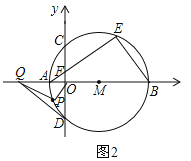
(2)动点P在⊙M的圆周上运动.①如图1,当EP平分∠AEB时,求PN×EP的值;②如图2,过点D作⊙M的切线交x轴于点Q,当点P与点A,B不重合时,![]() 是否为定值?若是,请求出其值;若不是,请说明理由.
是否为定值?若是,请求出其值;若不是,请说明理由.

【答案】(1) ⊙M的半径是5;(2)①PN·PE=50; ②![]() 是定值,理由见详解.
是定值,理由见详解.
【解析】
(1)由垂径定理可知OD=4,连接MD在Rt△OMD中用勾股定理即可求出r.
(2)①连接AP、BP.当EP平分∠AEB时,可得△BAP为等腰直角三角形,求出AP=![]() ,再证△APN∽△EPA得到PN·PE= PA2,进而可得PN×EP的值;
,再证△APN∽△EPA得到PN·PE= PA2,进而可得PN×EP的值;
②![]() 是定值.由DQ与⊙M于D点,可得△QMD∽△MDO,又MD=MP,可得
是定值.由DQ与⊙M于D点,可得△QMD∽△MDO,又MD=MP,可得![]() ,进而证明△QMP∽△PMQ,即可由相似三角形性质求解.
,进而证明△QMP∽△PMQ,即可由相似三角形性质求解.
(1)如图1:
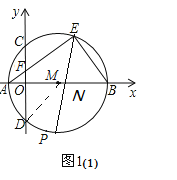
∵直径AB⊥CD,CD=8,
∴OD=![]() CD=4,
CD=4,
连接MD设MD=MA=r,
在Rt△OMD中.由OM2+OD2=MD2,
得(r﹣2)2+42=r2.解得r=5,
∴⊙M的半径是5;
(2)①如图1(2)
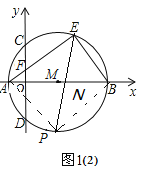
∵![]() .
.
∴![]() ,
,
∴AE=CD=8,
∵AB是直径,
∴∠AEB=90°,
连接AP,BP,
当EP平分∠AEB时,∠BAP=∠BEP=∠AEP=∠ABP=45°,
△BAP为等腰直角三角形,
∵AB=10,
∴AP=![]() ,
,
∵∠PAN=∠PEB=∠AEP, ∠APN=∠EPA,
∴△APN∽△EPA,
∴![]() ,
,
∴PN·PE= PA2=(![]() )2=50;
)2=50;
②![]() 是定值.
是定值.
理由如图2:连接PM、DM,
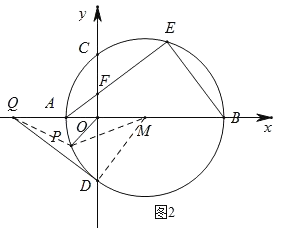
∵DQ与⊙M于D点,
∴∠MDQ=90°=∠DOM,
∴∠QMD=∠DMO,
∴△QMD∽△MDO,
∴![]() ,
,
又∵MD=MP,
∴![]() ,
,
又∵∠OMP=∠PMQ,
∴△QMP∽△PMQ,
∴![]() .
.

 阅读快车系列答案
阅读快车系列答案