题目内容
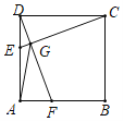
【题目】如图,边长为2的正方形ABCD中,点E、F分别在AD、AB上(点E不与点D重合),DE=AF,DF、CE交于点G,则AG的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】D
【解析】
通过证明△DEC≌△AFD得出∠DGE=90°,可知△DGC是直角三角形,则G点运动轨迹是以DC为直径的圆上,设圆的圆心为O,当A、G、O三点共线时,AG最短.由点E不与点D重合可得AG<2.
解:∵AD=DC,∠EDC=∠FAD,DE=AF,
∴△DEC≌△AFD(SAS).
∴∠DCE=ADF.
∵∠DCE+∠DEC=90°,
∴∠ADF+∠DEC=90°,即∠DGE=90°=∠DGC.
所以点G运动的轨迹在以DC为直径的圆上的一段弧,圆心在DC中点O处.
当A、G、O三点共线时,AG最短,如图所示.
此时AO=![]() =
=![]() =
=![]() ,OG=
,OG=![]() DC=1,
DC=1,
所以AG=AO-OG=![]() -1.
-1.
因为点E不与点D重合,所以AG<2.
所以![]() -1≤AG<2.
-1≤AG<2.
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目