题目内容
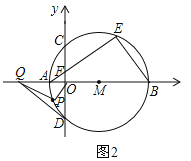
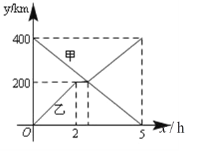
【题目】甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲,乙两车与B地的路程分别为y甲(km),y乙 (km),行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题:
(1)乙车休息了多长时间;
(2)求乙车与甲车相遇后y乙与x的函数解析式,并写出自变量x的取值范围;
(3)当两车相距40km时,求出x的值.
【答案】(1)乙车休息了0.5 h;(2)y乙=80x(2.5≤x≤5);(3)x=2或x=![]()
【解析】
(1)由图可知,乙车休息的时间=甲车行驶200km的时间-2,先求出甲车的速度,然后可设乙车休息的时间为t小时,利用200+甲车行驶(t+2)小时的路程=400,解得t值,或用算术方法求解即可;
(2)根据待定系数法,可相遇后y乙与x的函数解析式;
(3)分类讨论,由相遇前y甲-y乙=40,相遇后y乙-y甲=40即可求得x值.
(1)方法1:设乙车休息了t小时,根据题意得
200﹢![]() ·(t﹢2)=400,解得t=0.5,即乙车休息了0.5 h;
·(t﹢2)=400,解得t=0.5,即乙车休息了0.5 h;
方法2:(400-200)÷![]() -2=0.5(h),即乙车休息了0.5 h ;
-2=0.5(h),即乙车休息了0.5 h ;
(2)设y乙与x的函数解析式为y乙=kx﹢b,把(2.5,200)、(5,400)代入,得
![]() ,解得
,解得![]() ,
,
∴乙车与甲车相遇后y乙与x的函数解析式为:y乙=80x(2.5≤x≤5).
(3)由200÷2=100km∕h得
乙车与甲车相遇前y乙与x的函数解析式为:y乙=100x(0≤x﹤2.5).
∴相遇前:100x﹢80x﹢40=400,解得x=2;
相遇后:80x﹢200﹢80(x﹣2.5)=440,解得x=![]() .
.
综上可知,x=2或x=![]() .
.

【题目】2020年是5G爆发元年,三大运营商都在政策的支持下,加快着5G建设的步伐.某通信公司实行的5G畅想套餐,部分套餐资费标准如下:
套餐类型 | 月费(元/月) | 套餐内包含内容 | 套餐外资费 | ||
国内数据流量(GB) | 国内主叫(分钟) | 国内流量 | 国内主叫 | ||
套餐1 | 128 | 30 | 200 | 每5元1GB,用满3GB后每3元1GB,不足部分按照0.03/元MB收取 | 0.19元/分钟 |
套餐2 | 158 | 40 | 300 | ||
套餐3 | 198 | 60 | 500 | ||
套餐4 | 238 | 80 | 600 | ||
小武每月大约使用国内数据流量49GB,国内主叫350分钟,若想使每月付费最少,则他应预定的套餐是( )
A.套餐1B.套餐2C.套餐3D.套餐4