Question

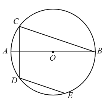
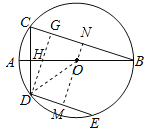
【题目】如图，AB是⊙O的直径，弦CD⊥AB，DE∥CB．若AB＝10，CD＝6，则DE的长为 （ ）

A.B.C.6D.

Answer 1

【答案】A

【解析】

设AB与CD交于H，连接OD，作OM⊥DE，交BC于N，作DG⊥BC，根据垂径定理得出CH=DH，DM=EM，BN=CN，利用勾股定理求得OH，即可求得BH，进而求得BC，求得ON，根据三角形函数求得DG，因为MN=DG，即可求得OM，根据勾股定理求得DM，得出DE．

解：设AB与CD交于H，连接OD，作OM⊥DE，交BC于N，作DG⊥BC，

∵DE∥BC，

∴MN⊥BC，DG⊥DE，

∴四边形DMNG是矩形，

∴DG=MN，

∵OM⊥DE，ON⊥BC，

∴DM=EM=DE，BN=CN，

∵AB是⊙O的直径，弦CD⊥AB，弦DE∥CB．

∴CH=DH=CD=3，

∴OH==4，

∴BH=9，

∴BC==3，

∴BN=BC=，

∴ON=，

∵sin∠BCH=，即，

∴DG=，

∴MN=DG=，

∴OM=MN-ON=，

∴DM==，

∴DE=2DM=．

故选A．