ЬтФПФкШн
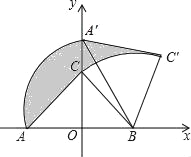
ЁОЬтФПЁПЃЈБОЬт10ЗжЃЉШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯп![]() гыyжсНЛгкЕуCЃЌгыxжсНЛгкЕуBЃЌХзЮяЯп
гыyжсНЛгкЕуCЃЌгыxжсНЛгкЕуBЃЌХзЮяЯп![]() ОЙ§BЁЂCСНЕуЃЌгыxжсЕФе§АыжсНЛгкСэвЛЕуAЃЌЧвOA ЃКOC="2" ЃК7ЃЎ
ОЙ§BЁЂCСНЕуЃЌгыxжсЕФе§АыжсНЛгкСэвЛЕуAЃЌЧвOA ЃКOC="2" ЃК7ЃЎ
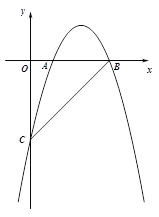


ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
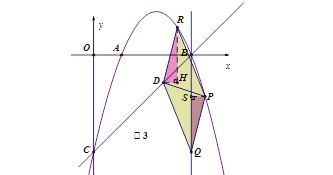
ЃЈ2ЃЉЕуDЮЊЯпЖЮCBЩЯЃЌЕуPдкЖдГЦжсЕФгвВрХзЮяЯпЩЯЃЌPD=PBЃЌЕБtanЁЯPDBЃНЃВЃЌЧѓPЕуЕФзјБъЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕуQЃЈ7ЃЌmЃЉдкЕкЫФЯѓЯоФкЃЌЕуRдкЖдГЦжсЕФгвВрХзЮяЯпЩЯЃЌШєвдЕуPЁЂDЁЂQЁЂRЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃЌЧѓЕуQЁЂRЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃН-![]() xЃВЃЋ
xЃВЃЋ![]() x-7 ЃЛЃЈ2ЃЉPЃЈ8ЃЌ-3ЃЉЃЛ
x-7 ЃЛЃЈ2ЃЉPЃЈ8ЃЌ-3ЃЉЃЛ
ЃЈ3ЃЉRЃЈ10ЃЌ-12ЃЉ,QЃЈ7ЃЌ-11ЃЉЛђRЃЈ6ЃЌ2ЃЉЃЌQЃЈ7ЃЌ-7ЃЉ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгажБЯпНтЮіЪНПЩвдЧѓГіCЕуЕФзјБъЃЌдйРћгУOA ЃКOC="2" ЃК7ЃЎЧѓГіAЕФзјБъ.зюКѓАбAЁЂCДњШыХзЮяЯпНтЮіЪНЧѓГіМДПЩ.
ЃЈ2ЃЉЯШЧѓГіBЕФзјБъПЩЕУЁЯOCB=ЁЯOBC=45ЁуЃЌгжЙ§PзїPEЁЭBCгкЕуEЃЌЫљвдЁЯCFG=ЁЯOCB==45ЁуОЭЕУЕНЯпЖЮEFЁЂBFЁЂEPЕФЪ§СПЙиЯЕЃЛгжtanЁЯPDBЃНЃВПЩвдЕУЕНЯпЖЮEPЁЂDEЁЂPDЕФЪ§СПЙиЯЕЃЌШЛКѓЩшГіPЁЂFЕФзјБъРћгУЫћУЧЕФзнзјБъЯрЕШМДПЩЧѓГіЕуЕФзјБъЃЛ
ЃЈ3ЃЉШєвдЕуPЁЂDЁЂQЁЂRЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮгаСНжжЧщПіЃКЯпЖЮPDгаПЩФмЪЧБпвВгаПЩФмЪЧЖдНЧЯп.
ЕБPDЪЧБпЪБЃЌМДDPЁЮQRЪБЃЌЁпBЃЈ7ЃЌ0ЃЉЃЌQЃЈ7ЃЌnЃЉЁрBQЁЮyжс
Й§PзїPNЁЮBQЃЌЙ§DзїDNЁЭBQНЛPNгкЕуNЃЌЙ§RзїRMЁЭBQгкЕуM. ЩшPDНЛBQгкЕуTЃЌDNНЛBMгкЕуI
МДПЩжЄУїЁїRMQЁеЁїDNPЃЌдйЧѓГіDЕуЕФзјБъЃЌЩшRЕуЕФКсзјБъЮЊtЃЌЁпRM=DNЃЌЁрt-7=8-5НтЕУt=10ЃЌдйАбt=10ДјШыХзЮяЯпМДПЩЧѓГіRЁЂQЃЛЕБPDЪЧЖдНЧЯпЪБЃЌЭЌРэЧѓГі.
ЪдЬтНтЮіЃКЃЈ1ЃЉЁпжБЯпy=kx-7гыyжсЕФИКАыжсНЛгкЕуC ЁрCЃЈ0ЃЌ-7ЃЉ ЁрOC=7
ЁпХзЮяЯпy=ax2+bx+14aОЙ§ЕуCЃЌЁр14a=-7ЃЌЁрa =-![]() ЁрyЃН-
ЁрyЃН-![]() xЃВЃЋbx-7
xЃВЃЋbx-7
ЁпOA ЃКOC="2" ЃК7ЃЎЁрOA=2ЃЌЁрAЃЈ2ЃЌ0ЃЉЁпХзЮяЯпyЃН-![]() xЃВЃЋbx-7ОЙ§ЕуA
xЃВЃЋbx-7ОЙ§ЕуA
Ёрb=![]() ЁрХзЮяЯпЕФНтЮіЪНЮЊyЃН-
ЁрХзЮяЯпЕФНтЮіЪНЮЊyЃН-![]() xЃВЃЋ
xЃВЃЋ![]() x-7
x-7

ЃЈ2ЃЉШчЭМ1ЃЌЁпХзЮяЯпyЃН-![]() xЃВЃЋ
xЃВЃЋ![]() x-7ОЙ§BЕуЃЌ Сюy=0НтЕУx=7Лђx=2ЃЈЩсЃЉЁрBЃЈ7ЃЌ0ЃЉ
x-7ОЙ§BЕуЃЌ Сюy=0НтЕУx=7Лђx=2ЃЈЩсЃЉЁрBЃЈ7ЃЌ0ЃЉ
ЁрOB=7ЁрOC=OBЁрЁЯOCB=ЁЯOBC=45Ёу
Й§ЕуPзїPFЁЭxжсгкЕуGЃЌНЛCBбгГЄЯпгкЕуFЃЌ
дђPFЁЮyжсЃЌЁрЁЯCFG=ЁЯOCB==45Ёу
ЁрBF=![]() GF
GF
Й§PзїPEЁЭBCгкЕуEЃЌ
ЁпPD=PB
ЁрЁЯPBD=ЁЯPDB
ЁрtanЁЯPBD=tanЁЯPDB=2
ЁрPE=2BE
ЁпEF=PE ЁрBF=BE
ЁрPF=![]() PE=2
PE=2![]() BE=2
BE=2![]() BF=4GFЃЌ
BF=4GFЃЌ
ЁрPG="3GF"
ЁпжБЯпy=kx-7Й§BЕу Ёрk=1 Ёрy=x-7
ЩшFЃЈ![]() ЃЉЃЌдђPЃЈ
ЃЉЃЌдђPЃЈ![]() ЃЉ
ЃЉ
вђЮЊЕуPдкХзЮяЯпyЃН-![]() xЃВЃЋ
xЃВЃЋ![]() x-7ЩЯЃЌ
x-7ЩЯЃЌ
ЫљвдЃЌ![]()
НтЕУm=7ЃЈЩсЃЉЛђm=8
ЁрPЃЈ8ЃЌ-3ЃЉ

ШчЭМ2,ЕБDPЁЮQRЪБЃЌМДЫФБпаЮDQRPЪЧЦНааЫФБпаЮ ЁпBЃЈ7ЃЌ0ЃЉЃЌQЃЈ7ЃЌnЃЉЁрBQЁЮyжс
Й§PзїPNЁЮBQЃЌЙ§DзїDNЁЭBQНЛPNгкЕуNЃЌ
Й§RзїRMЁЭBQгкЕуM.
ЩшPDНЛBQгкЕуTЃЌDNНЛBMгкЕуI
ЁрЁЯDTB=ЁЯDPNЃЌЁЯPTQ=ЁЯRQM, ЁпЁЯDTB=ЁЯPTQ
ЁрЁЯDPN=ЁЯRQM
ЁпЫФБпаЮDPRQЪЧЦНааЫФБпаЮ
ЁрDP=RQ
ЁпЁЯRMQ=ЁЯDNPЃЌЁрЁїRMQЁеЁїDNP
ЁрRM=DNЃЌMQ=PN
гЩЃЈ2ЃЉПЩЧѓFЃЈ8ЃЌ1ЃЉЃЌGF=1ЃЌBD=2BE=![]() BF=
BF=![]()
ЁпЁЯQBC=45ЁуЃЌЁрBI=DI=2 ЁрDЃЈ5ЃЌ-2ЃЉ
ЩшRЕуЕФКсзјБъЮЊtЃЌЁпRM=DNЃЌЁрt-7=8-5
НтЕУt=10
ЁпЕуRдкХзЮяЯпyЃН-![]() xЃВЃЋ
xЃВЃЋ![]() x-7 ЩЯЃЌ
x-7 ЩЯЃЌ
ЁрЕБt=10ЪБЃЌ![]()
ЁрRЃЈ10,-12ЃЉ
ЁпMQ=PN
Ёр3-2=-12-nЃЌЁрn=-11
ЁрRЃЈ10ЃЌ-12ЃЉ,QЃЈ7ЃЌ-11ЃЉ
ШчЭМ3ЃЌЕБDRЁЮQPЪБЃЌМДЫФБпаЮDQPRЪЧЦНааЫФБпаЮ
ЭЌРэПЩЧѓЕУRЃЈ6ЃЌ2ЃЉЃЌQЃЈ7ЃЌ-7ЃЉ

 ПьНнгЂгяжмжмСЗЯЕСаД№АИ
ПьНнгЂгяжмжмСЗЯЕСаД№АИЁОЬтФПЁП6дТ14ШеЪЧЁАЪРНчЯзбЊШеЁБЃЌФГЪаВЩШЁзддИБЈУћЕФЗНЪНзщжЏЪаУёвхЮёЯзбЊЃЎЯзбЊЪБвЊЖдЯзбЊепЕФбЊаЭНјааМьВтЃЌМьВтНсЙћгаЁАAаЭЁБЁЂЁАBаЭЁБЁЂЁАABаЭЁБЁЂЁАOаЭЁБ4жжРраЭЃЎдкЯзбЊепШЫШКжаЃЌЫцЛњГщШЁСЫВПЗжЯзбЊепЕФбЊаЭНсЙћНјааЭГМЦЃЌВЂИљОнетИіЭГМЦНсЙћжЦзїСЫСНЗљВЛЭъећЕФЭМБэЃК
бЊаЭ | A | B | AB | O |
ШЫЪ§ | ЁЁ ЁЁ | 10 | 5 | ЁЁ ЁЁ |
ЃЈ1ЃЉетДЮЫцЛњГщШЁЕФЯзбЊепШЫЪ§ЮЊЁЁ ЁЁШЫЃЌm=ЁЁ ЁЁЃЛ
ЃЈ2ЃЉВЙШЋЩЯБэжаЕФЪ§ОнЃЛ
ЃЈ3ЃЉШєетДЮЛюЖЏжаИУЪага3000ШЫвхЮёЯзбЊЃЌЧыФуИљОнГщбљНсЙћЛиД№ЃК
ДгЯзбЊепШЫШКжаШЮГщШЁвЛШЫЃЌЦфбЊаЭЪЧAаЭЕФИХТЪЪЧЖрЩйЃПВЂЙРМЦет3000ШЫжаДѓдМгаЖрЩйШЫЪЧAаЭбЊЃП