Question

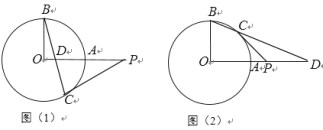
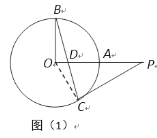
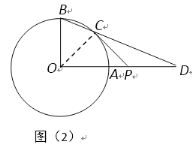
【题目】在⊙O中，半径OA丄OB，点D在OA或OA的延长线上（不与点O，A重合），直线BD交⊙O于点C，过C作⊙O的切线交直线OA于点P.

（1）如图（1），点D在线段OA上，若∠OBC=15°， 求∠OPC的大小；

（2）如图（2），点D在OA的延长线上，若∠OBC=65°，求∠OPC的大小.

Answer 1

【答案】（1）30°；（2）50°

【解析】

（1）连接OC，求出∠AOC=∠BOC - ∠BOA=60°，即可得到∠OPC=90° -∠AOC=30°；

（2）连接OC，求出∠AOC=∠AOB -∠BOC=40°，即可得到∠OPC=90° - ∠AOC = 50°.

解:（1）如图（1），连接OC.

∵PC是⊙O的切线，OC为⊙O的半径，

∴ OC⊥PC，

∴∠OCP=90°.

∵ OB=OC，

∴∠OCB=∠OBC=15°.

∴∠BOC=180° -∠OBC-∠OCB=150°.

∵ OB⊥OA，

∴∠BOA=90°.

∴∠AOC=∠BOC - ∠BOA=60°.

∴∠OPC=90° - ∠AOC=30°.

（2）如图（2），连接OC.

∵ CP是⊙O的切线，OC为⊙O的半径，

∴ OC⊥PC.

∴∠OCP = 90°.

∵ OB=OC，

∴∠OCB=∠OBC=65°.

∴∠BOC=180° -∠OBC -∠OCB=50°.

∵ OB⊥OA，

∴∠BOA=90°.

∴∠AOC=∠AOB -∠BOC=40°.

∴ ∠OPC=90° - ∠AOC = 50°.