Question

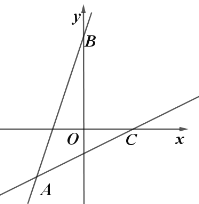
【题目】在平面直角坐标系中，抛物线（）与轴交于A、B两点（点B在A的右侧），与轴交于点C，D是抛物线的顶点.

（1）当时，求顶点D 的坐标

（2）若OD = OB，求的值；

（3）设E为A，B两点间抛物线上的一个动点（含端点A，B），过点E作EH⊥轴，垂足为H，交直线BC于点F. 记线段EF的长为t，若t的最大值为，求的值.

Answer 1

【答案】（1）D（1，4）；（2）；（3）

【解析】

（1）把代入解析式可求出解析式,再把解析式化为顶点式即可求得结果.

（2）令y=0可得出,,即可得到A,B的坐标,再把一般式化为顶点式可得到顶点坐标D,根据勾股定理可得,再根据OD = OB列出等式即可求出结果.

（3）设经过点B，C 的直线为把点代入可得到,再设点E（，）在抛物线（）上,可得点F（，）, 根据A（，），B（，），点E 在点A，B间的抛物线上,知道线段EF的长有两种情况,分别是当 时和当 时,即可求出结果.

（1）解：∵ ，∴ .

由,

∴ 顶点D/span>（1，4）.

（2）解：当时,有,即,

解得,.

∴ A（，）,B（，）.

∴ OB =3.

∵ .

∴ D（，）.

根据勾股定理，有.

∵ OD=OB，∴ .

解得 ,（舍）,

∴ .

（3）解：设经过点B，C 的直线为.

把点 B（，），C（，）代入,得.

设点E（，）在抛物线（）上,

有,点F（，）.

∵ A（，），B（，），点E 在点A，B间的抛物线上.

∴ 线段EF的长有两种情况:

①当 时,

∴ EF =t =.

∵ ,,

∴ 有最大值.

即 当时，t的最大值是.

②当 时,

∴ EF =t =.

∵ ，

∴ 当 时，随的增大而减小.

∴ 当时，的值最大，最大值是.

∵ ，∴.

∵ 当时，的最大值是.

∴ . 即.