题目内容
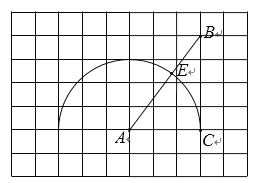
【题目】如图,在每个小正方形的边长为![]() 的网格中,点A,B,C在格点上,以点A为圆心、AC为半径的半圆交AB于点 E.
的网格中,点A,B,C在格点上,以点A为圆心、AC为半径的半圆交AB于点 E.
(1)BE的长为________;
(2)请用无刻度的直尺,在如图所示的网格中,找一点P(点P,C 在AB两侧),使PA=5,PE与半圆相切. 简要说明点P的位置是如何找到的.
【答案】(1)2;(2)图见解析,理由见解析.
【解析】
(1)先结合网格的特点可得![]() ,再根据勾股定理可得
,再根据勾股定理可得![]() ,然后根据圆的性质可得
,然后根据圆的性质可得![]() ,最后根据线段的和差即可得;
,最后根据线段的和差即可得;
(2)取格点![]() ,分别作直线
,分别作直线![]() ,两直线相交于点P,点P即为所作;理由:先根据平行四边形的判定与性质得出
,两直线相交于点P,点P即为所作;理由:先根据平行四边形的判定与性质得出![]() ,再根据三角形全等的判定定理与性质得出
,再根据三角形全等的判定定理与性质得出![]() ,然后根据三角形中位线定理、垂直平分线的判定与性质可得
,然后根据三角形中位线定理、垂直平分线的判定与性质可得![]() ,由此即可得证.
,由此即可得证.
(1)由网格的特点得:![]()
![]()
由圆的性质得:![]()
![]()
故答案为:2;
(2)如图,取格点![]() ,分别作直线
,分别作直线![]() ,两直线相交于点P,则点P即为所作,理由如下:
,两直线相交于点P,则点P即为所作,理由如下:
由网格的特点得:![]() ,
,![]() ,
,![]()
![]() 四边形ABGF是平行四边形
四边形ABGF是平行四边形
![]()
在![]() 和
和![]() 中,
中,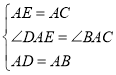
![]()
![]() ,即
,即![]()
![]() 与半圆相切
与半圆相切
![]() ,即点A是DF的中点,且
,即点A是DF的中点,且![]()
![]() 是
是![]() 的中位线,点E是DP的中点
的中位线,点E是DP的中点
![]() 垂直平分DP
垂直平分DP
![]()
综上,点P即为所作.


练习册系列答案
相关题目