题目内容
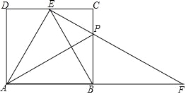
【题目】如图,在矩形ABCD中,AB=2,AD=![]() ,在边CD上有一点E,使EB平分∠AEC.若P为BC边上一点,且BP=2CP,连接EP并延长交AB的延长线于F.给出以下五个结论:
,在边CD上有一点E,使EB平分∠AEC.若P为BC边上一点,且BP=2CP,连接EP并延长交AB的延长线于F.给出以下五个结论:
①点B平分线段AF;②PF=![]() DE;③∠BEF=∠FEC;④S矩形ABCD=4S△BPF;⑤△AEB是正三角形.
DE;③∠BEF=∠FEC;④S矩形ABCD=4S△BPF;⑤△AEB是正三角形.
其中正确结论的序号是.
【答案】①②③⑤
【解析】
试题分析:∵四边形ABCD为矩形,∴AB∥CD,∴∠CEB=∠ABE,又∵BE平分∠AEC,
∴∠AEB=∠CEB,∴∠AEB=∠ABE,∴AE=AB=2,在Rt△ADE中,AD=![]() ,AE=2,由勾股定理可求得DE=1,∴CE=CD﹣DE=2﹣1=1,∵DC∥AB,∴△PCE∽△PBF,∴
,AE=2,由勾股定理可求得DE=1,∴CE=CD﹣DE=2﹣1=1,∵DC∥AB,∴△PCE∽△PBF,∴![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
∴BF=2,∴AB=BF,∴点B平分线段AF,故①正确;∵BC=AD=![]() ,∴BP=
,∴BP=![]()
![]() ,
,
在Rt△BPF中,BF=2,由勾股定理可求得PF=![]() =
=![]() =
=![]()
![]() ,
,
∵DE=1,∴PF=![]()
![]() DE,故②正确;在Rt△BCE中,EC=1,BC=
DE,故②正确;在Rt△BCE中,EC=1,BC=![]() ,由勾股定理可求得BE=2,
,由勾股定理可求得BE=2,
∴BE=BF,∴∠BEF=∠F,又∵AB∥CD,∴∠FEC=∠F,∴∠BEF=∠FEC,
故③正确;∵AB=2,AD=![]() ,∴S矩形ABCD=AB×AD=2×
,∴S矩形ABCD=AB×AD=2×![]() =2
=2![]() ,
,
∵BF=2,BP=![]()
![]() ,∴S△BPF=
,∴S△BPF=![]() BF×BP=
BF×BP=![]() ×2×
×2×![]()
![]() =
=![]()
![]() ,
,
∴4S△BPF=![]()
![]() ,∴S矩形ABCD=≠4S△BPF,故④不正确;
,∴S矩形ABCD=≠4S△BPF,故④不正确;
由上可知AB=AE=BE=2,∴△AEB为正三角形,故⑤正确;
综上可知正确的结论为:①②③⑤.
故答案为:①②③⑤.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目