题目内容
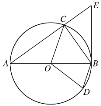
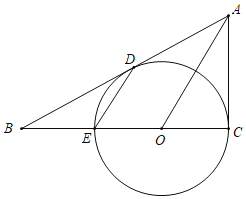
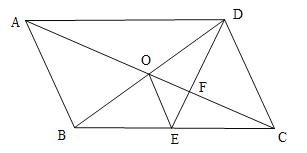
【题目】如图,已知ABCD的对角线AC,BD交于点O,DE平分∠ADC交BC于点E,交AC与点F,且∠BCD=60°,BC=2CD,连接OE,则下列结论:①OE∥AB ②SABCD=BD·CD ③AO=2BO ④S△DOF=2S△EOF,其中成立的有( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
①先根据题意说明BE=CE、OA=OC,然后根据三角形中位线定理即可判断;
②只要说明BD⊥CD即可判定为正确;
③设AB=x,分别表示OA和OB的长,然后进行比较即可判断;
④利用平行线分线段成比例定理可得DF=2EF,然后根据三角形的面积公式即可判定.
解:①∵四边形ABCD是平行四边形
∴AD//BC,OA=OC,∠ADC+∠BCD=180°
∵∠BCD=60°,
∴ADC= 120°,
∵DE平分∠ADC,
∴∠CDE=∠BCD=60°
∴△CDE等边三角形
∴CE=CD
∵BC=2CD
∴BE=CE
∵OA=OC
.∴OE//AB
故①正确;
②∵△DEC是等边三角形,
∴∠DEC=60°=∠DBC+∠BDE
∵BE=EC=DE
∴∠DBC=∠BDE=30°,
∴∠BDC=30°+60°=90°
∴BD⊥CD
∴S平行四边形ABCD=2![]() =2×
=2×![]() BD·CD= BD·CD;
BD·CD= BD·CD;
故②正确;
③设AB=x,则AD=2x,BD=![]() x,
x,
∴OB=![]() x
x
则由勾股定理可得: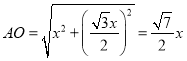
故③不正确;
④∵AD//EC,
∴![]()
∴DF=2EF
∵S△DOF和S△EOF的高相同
∴S△DOF=2S△EOF
故④正确;即共有3个正确.
故选C.

练习册系列答案
相关题目