题目内容
【题目】已知,在平面直角坐标系中,![]() 为坐标原点,抛物线
为坐标原点,抛物线![]()
![]() 分别交
分别交![]() 轴于
轴于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的侧),与
的侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)如图1,求![]() 的值;
的值;

(2)如图2,![]() 是
是![]() 轴上一点(不与点
轴上一点(不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的平行线,交抛物线于点
轴的平行线,交抛物线于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
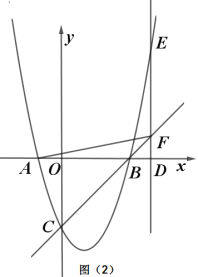
①当点![]() 在点
在点![]() 右侧时,连接AF,当
右侧时,连接AF,当![]() 时,求
时,求![]() 的长.
的长.
②当点![]() 在运动时,若
在运动时,若![]() 、
、![]() 、
、![]() 中有两条线段相等,此时点
中有两条线段相等,此时点![]() 的坐标_________.
的坐标_________.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() 的坐标为
的坐标为![]() ,
,![]() .
.
【解析】
(1)由ax2ax3a=0,可得A(1,0),B(3,0),OA=1,再根据tan∠ACO=![]() ,可求得C(0,3),即可求出a的值;
,可求得C(0,3),即可求出a的值;
(2)①构造全等三角形![]() ,由此AD=ED,设
,由此AD=ED,设![]() ,建立方程求解;
,建立方程求解;
②分两种情况讨论,分别建立方程进行求解即可得到答案.
(1)![]()
![]()
令![]() ,即
,即![]() ,解得
,解得![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]()
又∵![]() ,
,
∴![]() ;
;
(2)①由(1)得抛物线![]() ,BC所在直线
,BC所在直线![]() ,
,
设![]() ,
,
∴![]() ,
,![]()
∵![]() ,
,![]() 轴,
轴,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
又∵![]() ,
,
∴![]() ,
,
∴![]() 而
而![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
②当![]()
![]()
![]() ,
,
∴![]() ,∴
,∴![]()
当![]()
![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴D(-2,0),
综上,![]() 的坐标为
的坐标为![]() ,
,![]()

练习册系列答案
相关题目