题目内容
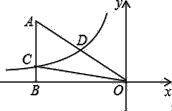
【题目】如图,已知A(2 ![]() ,2)、B(2
,2)、B(2 ![]() ,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(﹣2
,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(﹣2 ![]() ,2
,2 ![]() )的位置,则图中阴影部分的面积为 .
)的位置,则图中阴影部分的面积为 . 
【答案】![]() π
π
【解析】解:∵A(2 ![]() ,2)、A′(﹣2
,2)、A′(﹣2 ![]() ,2
,2 ![]() ),
),
∴∠A′OA=45°+60°=105°,
∵将△AOB绕着点O逆时针旋转,使点A(2 ![]() ,2)旋转到点A′(﹣2,2
,2)旋转到点A′(﹣2,2 ![]() )的位置,B旋转到点B′位置,
)的位置,B旋转到点B′位置,
∴∠A′OA=∠B′OB=105°,
∵B(2 ![]() ,1),A′(﹣2
,1),A′(﹣2 ![]() ,2
,2 ![]() ),
),
∴B′点坐标为(﹣2 ![]() +1,2
+1,2 ![]() );
);
如图,设 ![]() 交OA′于C′,
交OA′于C′,
∵A(2 ![]() ,2)、B(2
,2)、B(2 ![]() ,1),
,1),
∴OA=4,OC=OB= ![]() .
.
根据旋转的性质可得,S△OB′C′=S△OBC ,
∴阴影部分的面积=S扇形A'OA﹣S扇形C'OC= ![]() ﹣
﹣ ![]() =
= ![]() π,
π,
所以答案是: ![]() π.
π.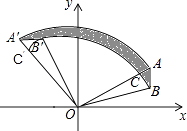
【考点精析】本题主要考查了旋转的性质的相关知识点,需要掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目