题目内容
【题目】已知关于x的一元二次方程x2+4x﹣k=0有两个不相等的实数根.
(1)求k的取值范围;
(2)请你在﹣5,﹣4,﹣3,1,2,3中选择一个数作为k的值,使方程有两个整数根,并求出方程的两个整数根.
【答案】
(1)
解:∵方程x2+4x﹣k=0有两个不相等的实数根,
∴△=42﹣4×1×(﹣k)=16+4k>0,
解得:k>﹣4,
∴k的取值范围为k>﹣4;
(2)
解:当k=﹣3时,△=16+4k=4,
原方程为x2+4x+3=(x+1)(x+3)=0,
解得:x=﹣1或x=﹣3;
当k=1时,△=16+4k=20,
![]() 不是整数;
不是整数;
当k=2时,△=16+4k=24,
![]() 不是整数;
不是整数;
当k=3时,△=16+4k=28,
![]() 不是整数.
不是整数.
∴当取k=﹣3时,方程的两个整数根为﹣1或﹣3.
【解析】(1)根据方程有两个不等实根结合根的判别式,可得出关于k的一元一次不等式,解不等式即可得出k的取值范围;(2)结合(1)的结论,找出k的值,并验证k为这些数时,何时方程的两根为整数,由此即可得出结论.
【考点精析】解答此题的关键在于理解求根公式的相关知识,掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
【题目】光明中学八年级甲、乙、丙三个班中,每班的学生人数都为40名,某次数学考试的成绩统计如图:(每组分数含最小值,不含最大值)
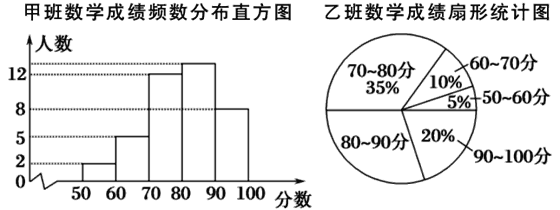
丙班数学成绩频数统计表
分数 | 50~60 | 60~70 | 70~80 | 80~90 | 90~100 |
人数 | 1 | 4 | 15 | 11 | 9 |
根据上图及统计表提供的信息,则80~90分这一组人数最多的班是________