题目内容
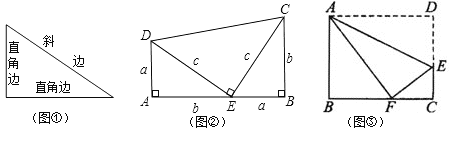
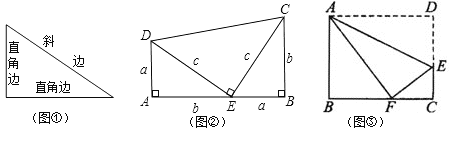
【题目】我们已经知道,有一个内角是直角的三角形是直角三角形.其中直角所在的两条边叫直角边,直角所对的边叫斜边(如图①所示).数学家已发现在一个直角三角形中,两个直角边边长的平方和等于斜边长的平方.如果设直角三角形的两条直角边长度分别是![]() 和
和![]() ,斜边长度是
,斜边长度是![]() ,那么可以用数学语言表达:
,那么可以用数学语言表达:![]() .
.
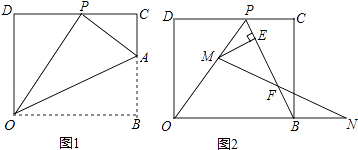
(1)在图②,若![]() ,
,![]() ,则
,则![]() ;
;
(2)观察图②,利用面积与代数恒等式的关系,试说明![]() 的正确性.其中两个相同的直角三角形边AE、EB在一条直线上;
的正确性.其中两个相同的直角三角形边AE、EB在一条直线上;
(3)如图③所示,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8,BC=10,利用上面的结论求EF的长.
【答案】(1)12; (2)答案见解析;(3)5
【解析】
试题
(1)利用题中所给公式:![]() ,代入
,代入![]() 即可解出
即可解出![]() 的值;
的值;
(2)先用“梯形面积计算公式”计算出图②的面积,再分别计算图②中三个三角形的面积并相加得到图②的面积,利用两次所求面积相等得到等式,把等式变形即可得到公式:![]() ;
;
(3)由矩形和折叠的性质可得:AF=AD=BC=10,DC=AB=8,EF=DE;在Rt△ABF中,由题中所给结论可计算出BF的长,从而可得FC的长;设EF=![]() ,则DE=
,则DE=![]() ,EC=
,EC=![]() ,这样在Rt△EFC中,由题中所给结论可得关于
,这样在Rt△EFC中,由题中所给结论可得关于![]() 的方程,解方程即可求得EF的长.
的方程,解方程即可求得EF的长.
试题解析:
(1)∵![]() ,代入
,代入![]() ,
,
∴![]() ;
;
(2)∵图①的面积=![]() =
=![]() ,
,
图①的面积=S梯形ABCD=![]() =
=![]() ,
,
∴ ![]() =
=![]() ,
,
∴![]() ,
,
即![]() .
.
(3)由四边形ABCD是矩形和折叠的性质可得,![]() ,
,![]() ,EF=DE,
,EF=DE,
由题意可得:在Rt△ABF中,![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
又∵![]() ,
,
∴ ![]() ,
,
设![]() ,则
,则![]() ,
, ![]() ,
,
∵在Rt△ECF中,![]() ,
,
∴![]() ,
,
解得 ![]() ,即
,即![]() .
.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案【题目】光明中学八年级甲、乙、丙三个班中,每班的学生人数都为40名,某次数学考试的成绩统计如图:(每组分数含最小值,不含最大值)
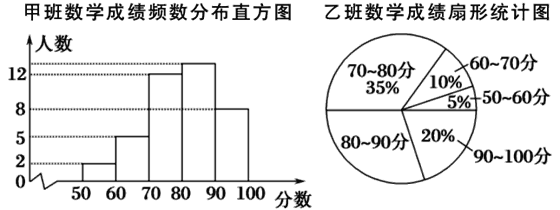
丙班数学成绩频数统计表
分数 | 50~60 | 60~70 | 70~80 | 80~90 | 90~100 |
人数 | 1 | 4 | 15 | 11 | 9 |
根据上图及统计表提供的信息,则80~90分这一组人数最多的班是________