题目内容
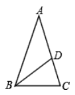
【题目】如图，在等腰三角形ABC中，AB=AC，点D为AC上一点，且AD=BD=BC，则等腰三角形ABC的顶角度数为__________________．
【答案】360
【解析】
由AB=AC，AD=BD=BC，根据等角对等边的知识，可得∠A=∠ABD，∠C=∠ABC=∠CDB，设∠A=x°，根据等腰三角形的性质得出∠ABD=x°，∠C=∠ABC=∠CDB=2x°，然后根据三角形的内角和定理得出关于x的方程，解方程即可求得答案．
∵AB=AC，AD=BD=BC，
∴∠A=∠ABD，∠C=∠ABC=∠CDB，
设∠A=x°,则∠ABD=∠A=x°，
∴∠C=∠ABC=∠CDB=∠A+∠ABD=2x°，
∵∠A+∠C+∠ABC=180°，
∴x+2x+2x=180，
解得x=36.
故等腰三角形ABC的顶角度数为36°.
故答案为：36°.
练习册系列答案
相关题目
【题目】根据如表回答下列问题：
x | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 | 16.9 | 17.0 |
x2 | 262.44 | 265.69 | 268.96 | 272.25 | 275.56 | 278.89 | 282.24 | 285.61 | 289 |
（1）275.56的平方根是______ ；
（2）
= ______ ；
（3）查看上表， <
< ．
