题目内容
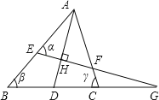
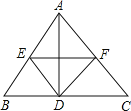
【题目】如图,等腰Rt△ABC中,∠C=90°,D为AC上一点,连接BD,将线段BD绕点D顺时针旋转90°得到线段DE,DE与AB相交于点F,过点D作DG⊥AB,垂足为点G.若EF=5,CD=2 ![]() ,则△BDG的面积为 .
,则△BDG的面积为 . 
【答案】96
【解析】解:过点E作EH⊥AC,垂足为H,连接AE. 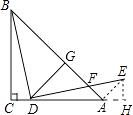
∵∠BDE=90°,
∴∠BDC+∠EDH=90°.
又∵∠CBD+∠CDB=90°,
∴∠CBD=∠EDH.
在△BCD和△DHE中, 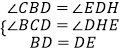 ,
,
∴△BCD≌△DHE.
∴BC=DH,CD=EH=2 ![]() .
.
∵△ABC为等腰直角三角形,
∴BC=CA.
∴AC=DH.
∴DC=AH=2 ![]() .
.
∴AH=EH=2 ![]() .
.
∴AE= ![]() =4.
=4.
∵∠BAC=45°,∠EAH=45°,
∴∠FAE=90°.
∴AF= ![]() =3.
=3.
∵∠BDF=∠FAE,∠BFD=∠EFA,
∴△BDF∽△EFA.
∴ ![]() .
.
设DF=x,则BD=DE=x+5.
∴ ![]() .
.
解得:x=15.
∴DF=15,BD=20.
∴BG= ![]() BD=16,DG=
BD=16,DG= ![]() =12.
=12.
∴ ![]() =
= ![]() =96.
=96.
故答案为;96.
过点E作EH⊥AC,垂足为H,连接AE.先依据AAS证明△BCD≌△DHE,从而得到BC=DH,CD=EH=2 ![]() ,由等腰直角三角形的性质可知BC=CA,从而可证明AH=EH=2
,由等腰直角三角形的性质可知BC=CA,从而可证明AH=EH=2 ![]() ,由勾股定理可知AE=4.在△EFA中由勾股定理可求得AF=3,由∠BDF=∠FAE,∠BFD=∠EFA可知△BDF∽△EFA,设DF=x,则BD=DE=x+5由相似三角形的性质可知:
,由勾股定理可知AE=4.在△EFA中由勾股定理可求得AF=3,由∠BDF=∠FAE,∠BFD=∠EFA可知△BDF∽△EFA,设DF=x,则BD=DE=x+5由相似三角形的性质可知: ![]() .解得:x=15.故此DF=15,BD=20,从而可求得BG=
.解得:x=15.故此DF=15,BD=20,从而可求得BG= ![]() BD=16,DG=
BD=16,DG= ![]() =12,最后依据三角形的面积公式求解即可.
=12,最后依据三角形的面积公式求解即可.

【题目】光明中学八年级甲、乙、丙三个班中,每班的学生人数都为40名,某次数学考试的成绩统计如图:(每组分数含最小值,不含最大值)
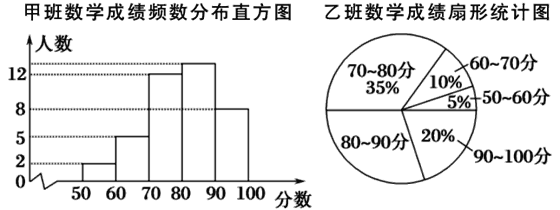
丙班数学成绩频数统计表
分数 | 50~60 | 60~70 | 70~80 | 80~90 | 90~100 |
人数 | 1 | 4 | 15 | 11 | 9 |
根据上图及统计表提供的信息,则80~90分这一组人数最多的班是________