题目内容
如图所示,直角梯形 的直角顶点
的直角顶点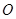 是坐标原点,边
是坐标原点,边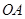 、
、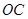 分别在
分别在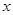 轴、
轴、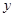 轴的正半轴上,
轴的正半轴上,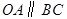 ,
,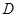 是
是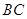 上一点,
上一点,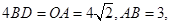
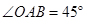 ,其中点
,其中点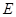 、
、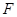 分别是线段
分别是线段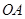 、
、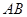 上的两个动点,且始终保持
上的两个动点,且始终保持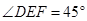 。
。
小题1:直接写出点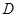 的坐标
的坐标
小题2:求证: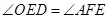 ;
;
小题3:当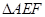 是等腰三角形时,△AEF关于直线EF的对称图形为
是等腰三角形时,△AEF关于直线EF的对称图形为 ,求
,求 与五边形OEFBC的重叠部分的面积.
与五边形OEFBC的重叠部分的面积.

备用图
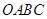 的直角顶点
的直角顶点 是坐标原点,边
是坐标原点,边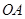 、
、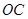 分别在
分别在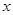 轴、
轴、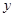 轴的正半轴上,
轴的正半轴上,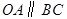 ,
,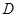 是
是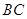 上一点,
上一点,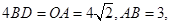
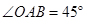 ,其中点
,其中点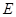 、
、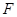 分别是线段
分别是线段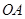 、
、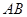 上的两个动点,且始终保持
上的两个动点,且始终保持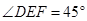 。
。小题1:直接写出点
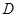 的坐标
的坐标小题2:求证:
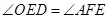 ;
;小题3:当
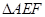 是等腰三角形时,△AEF关于直线EF的对称图形为
是等腰三角形时,△AEF关于直线EF的对称图形为 ,求
,求 与五边形OEFBC的重叠部分的面积.
与五边形OEFBC的重叠部分的面积.
备用图
小题1:解:
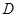
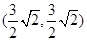 ..……..1分
..……..1分小题2:证明:由
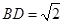 ,知
,知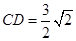 ,
,

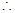
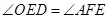
者利用外角证明:∠OEF=∠OED+∠DEF=∠A+∠EFA,∵∠DEF=∠A=45°,
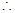
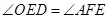 .……..3分
.……..3分小题3:解:分三种情况来计算:
第一种情况:
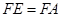 ,此时
,此时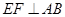 ,
,
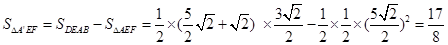 .……..4分
.……..4分第二种情况:
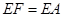 ,此时
,此时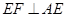 ,
, .……..5分
.……..5分第三种情况:
 ,
,此时△
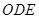 ,△
,△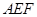 均为等腰三角形,
均为等腰三角形,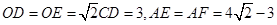
且可求
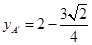 <
<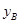 ,∴△
,∴△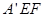 在五边形内部,
在五边形内部,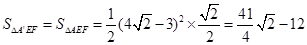 ..……..7分
..……..7分综上:
 =
=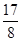 ,1,
,1,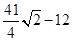 .
.(1)过B作x轴的垂线,设垂足为M,由已知易求得OA=4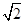 ,在Rt△ABM中,已知了∠OAB的度数及AB的长,即可求出AM、BM的长,进而可得到BC、CD的长,由此可求得D点的坐标;
,在Rt△ABM中,已知了∠OAB的度数及AB的长,即可求出AM、BM的长,进而可得到BC、CD的长,由此可求得D点的坐标;
(2)先求出∠OED、∠AFE与∠FEA的等量关系,从而得出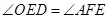 ;
;
(3)若△AEF是等腰三角形,应分三种情况讨论:
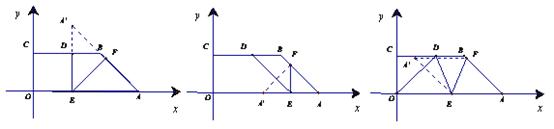
①AF=EF,此时△AEF是等腰Rt△,A′在AB的延长线上,重合部分是四边形EDBF,其面积可由梯形ABDE与△AEF的面积差求得;
②AE=EF,此时△AEF是等腰Rt△,且E是直角顶点,此时重合部分即为△A′EF,由于∠DEF=∠EFA=45°,得DE∥AB,即四边形AEDB是平行四边形,则AE=BD,进而可求得重合部分的面积;
③AF=AE,此时四边形AEA′F是菱形,重合部分是△A′EF;由(2)知:△ODE∽△AEF,那么此时OD=OE=3,由此可求得AE、AF的长,过F作x轴的垂线,即可求出△AEF中AE边上的高,进而可求得△AEF(即△A′EF)的面积.
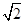 ,在Rt△ABM中,已知了∠OAB的度数及AB的长,即可求出AM、BM的长,进而可得到BC、CD的长,由此可求得D点的坐标;
,在Rt△ABM中,已知了∠OAB的度数及AB的长,即可求出AM、BM的长,进而可得到BC、CD的长,由此可求得D点的坐标;(2)先求出∠OED、∠AFE与∠FEA的等量关系,从而得出
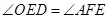 ;
;(3)若△AEF是等腰三角形,应分三种情况讨论:
①AF=EF,此时△AEF是等腰Rt△,A′在AB的延长线上,重合部分是四边形EDBF,其面积可由梯形ABDE与△AEF的面积差求得;
②AE=EF,此时△AEF是等腰Rt△,且E是直角顶点,此时重合部分即为△A′EF,由于∠DEF=∠EFA=45°,得DE∥AB,即四边形AEDB是平行四边形,则AE=BD,进而可求得重合部分的面积;
③AF=AE,此时四边形AEA′F是菱形,重合部分是△A′EF;由(2)知:△ODE∽△AEF,那么此时OD=OE=3,由此可求得AE、AF的长,过F作x轴的垂线,即可求出△AEF中AE边上的高,进而可求得△AEF(即△A′EF)的面积.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



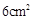 ,长为
,长为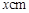 ,则这个矩形的宽
,则这个矩形的宽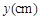 与长
与长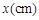 的函数关系为 。
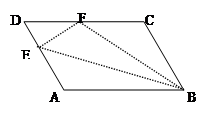
的函数关系为 。 中,点E在BC上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.
中,点E在BC上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数. 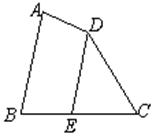
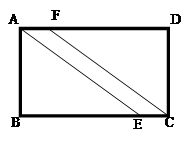
 以DE为折痕向右折叠,AE与BC交于点F,则
以DE为折痕向右折叠,AE与BC交于点F,则 的面积为( )
的面积为( )