题目内容
如图所示,有一条等宽(AF=EC)的小路穿过矩形的草地ABCD,已知AB="60m," BC="84m," AE=100m.
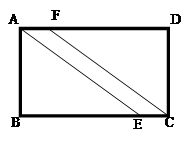
(1)试判断这条小路(四边形AECF)的形状,并说明理由;
(2)求这条小路的的面积和对角线FE的长度.(精确到整数)

(1)试判断这条小路(四边形AECF)的形状,并说明理由;
(2)求这条小路的的面积和对角线FE的长度.(精确到整数)
(1)四边形AECF是平行四边形,理由见解析(2)240,97
(1)四边形AECF是平行四边形,理由:--------2分
矩形ABCD中,AF∥EC--------3分
又AF=EC
∴四边形AECF是平行四边形-------4分
(2)在Rt△ABC中,AB="60," AE="100,"
根据勾股定理得BE=80-------6分
∴EC=BC-BE=4
所以这条小路的面积S=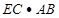 =4×60=240(m²)-------9分
=4×60=240(m²)-------9分
连结FE,过点F作FO⊥BC,垂足为O.则-------10分
FO=AB=60, BO=AF=4
OE=BE-BO=80-4=76-------11分
由勾股定理,得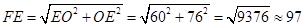 (m)-------13分
(m)-------13分
(1)考查平行四边形的判定,ABCD是矩形,则AF∥EC,又AF=CE,进而可判断其四边形的形状.
(2)面积的计算以及对角线的计算,面积可以利用底边长乘以高,对角线可通过勾股定理求解即可,
这一问属于纯粹的计算问题.
矩形ABCD中,AF∥EC--------3分
又AF=EC
∴四边形AECF是平行四边形-------4分
(2)在Rt△ABC中,AB="60," AE="100,"
根据勾股定理得BE=80-------6分
∴EC=BC-BE=4
所以这条小路的面积S=
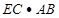 =4×60=240(m²)-------9分
=4×60=240(m²)-------9分连结FE,过点F作FO⊥BC,垂足为O.则-------10分
FO=AB=60, BO=AF=4
OE=BE-BO=80-4=76-------11分
由勾股定理,得
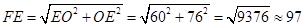 (m)-------13分
(m)-------13分(1)考查平行四边形的判定,ABCD是矩形,则AF∥EC,又AF=CE,进而可判断其四边形的形状.
(2)面积的计算以及对角线的计算,面积可以利用底边长乘以高,对角线可通过勾股定理求解即可,
这一问属于纯粹的计算问题.

练习册系列答案
相关题目

 的直角顶点
的直角顶点 是坐标原点,边
是坐标原点,边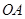 、
、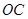 分别在
分别在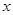 轴、
轴、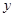 轴的正半轴上,
轴的正半轴上,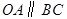 ,
,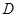 是
是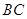 上一点,
上一点,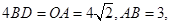
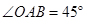 ,其中点
,其中点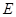 、
、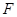 分别是线段
分别是线段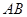 上的两个动点,且始终保持
上的两个动点,且始终保持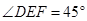 。
。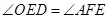 ;
; 是等腰三角形时,△AEF关于直线EF的对称图形为
是等腰三角形时,△AEF关于直线EF的对称图形为 ,求
,求
 中,
中, ,半径为1的动圆⊙
,半径为1的动圆⊙ 从
从 点出发,以每秒3个单位的速度沿折线
点出发,以每秒3个单位的速度沿折线 向终点
向终点 移动,设移动的时间为秒;同时,⊙
移动,设移动的时间为秒;同时,⊙ 的半径
的半径 不断增大,且
不断增大,且 (≥0).(1)当
(≥0).(1)当 秒时,两圆的位置关系是 ;(2)当t≥4秒时,若两圆外切,则t的值为 秒.
秒时,两圆的位置关系是 ;(2)当t≥4秒时,若两圆外切,则t的值为 秒. 
 中,
中, .第一次将纸片折叠,使点
.第一次将纸片折叠,使点 与点
与点 重合,折痕与
重合,折痕与 交于点
交于点 ;设
;设 的中点为
的中点为 第二次将纸片折叠使点
第二次将纸片折叠使点


 ;设
;设 的中点为
的中点为 ,
, ,… .按上述方法折叠,
,… .按上述方法折叠, 交于点
交于点 ,则
,则 = ▲ ,
= ▲ , = ▲ .
= ▲ .
 中,
中, ,且
,且 ,
, 的周长为14 ,将
的周长为14 ,将 的位置。
的位置。 的周长。
的周长。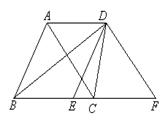
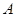 、
、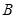 为直线
为直线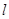 上两点,点
上两点,点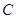 为直线
为直线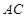 、
、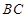 ,分别以
,分别以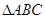 外作正方形
外作正方形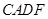 和正方形
和正方形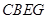 ,过点
,过点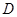 作
作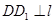 于点
于点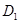 ,过点
,过点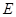 作
作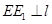 于点
于点 .
.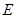 恰好在直线
恰好在直线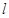 上时(此时
上时(此时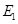 与
与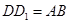 ;
;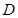 、
、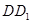 、
、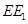 、
、 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
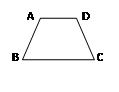
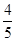 ,S△BCD=
,S△BCD=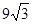 . 求四边形ABCD的周长.
. 求四边形ABCD的周长.