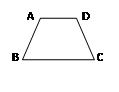题目内容
如图,矩形ABCD的边AB在y轴上,AB的中点与原点重合,AB=2,AD=1,过定点Q(2,0)和动点P(0,a)的直线与矩形ABCD的边有公共点,则a的取值范围是____________.

-2≤a≤2
∵O是AD的中点,∴OA=OD=1,∴C的坐标是(1,-1),D的坐标是(1,1).
设直线PC的解析式是:y=kx+b,根据题意得: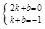 ,解得:
,解得: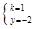 ,
,
则直线的解析式是:y=x-2,与y轴的交点坐标是(0,-2);
设直线PD的解析式是y=mx+n,根据题意得: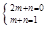 ,解得:
,解得: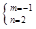 ,
,
则直线的解析式是:y=-x+2,与y轴的交点坐标是(0,2).
则a的取值范围是:-2≤a≤2.
设直线PC的解析式是:y=kx+b,根据题意得:
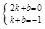 ,解得:
,解得: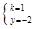 ,
,则直线的解析式是:y=x-2,与y轴的交点坐标是(0,-2);
设直线PD的解析式是y=mx+n,根据题意得:
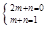 ,解得:
,解得: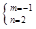 ,
,则直线的解析式是:y=-x+2,与y轴的交点坐标是(0,2).
则a的取值范围是:-2≤a≤2.

练习册系列答案
相关题目
 为
为 边的中点,连结DE并延长DE交AB延长线于F. 求证:
边的中点,连结DE并延长DE交AB延长线于F. 求证: .
.

 ,试求
,试求 的度数(7分)
的度数(7分)
 中,
中,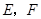 分别是边
分别是边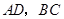 的中点,点
的中点,点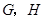 在
在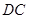 边上,且
边上,且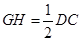 .若
.若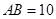 ,
,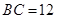 ,则图中阴影部分的面积为 .
,则图中阴影部分的面积为 .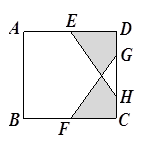

 的直角顶点
的直角顶点 是坐标原点,边
是坐标原点,边 、
、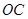 分别在
分别在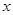 轴、
轴、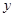 轴的正半轴上,
轴的正半轴上,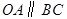 ,
,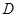 是
是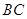 上一点,
上一点,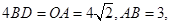
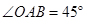 ,其中点
,其中点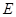 、
、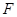 分别是线段
分别是线段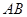 上的两个动点,且始终保持
上的两个动点,且始终保持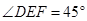 。
。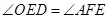 ;
;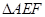 是等腰三角形时,△AEF关于直线EF的对称图形为
是等腰三角形时,△AEF关于直线EF的对称图形为 ,求
,求
 中,
中, ,半径为1的动圆⊙
,半径为1的动圆⊙ 从
从 点出发,以每秒3个单位的速度沿折线
点出发,以每秒3个单位的速度沿折线 向终点
向终点 移动,设移动的时间为秒;同时,⊙
移动,设移动的时间为秒;同时,⊙ 的半径
的半径 不断增大,且
不断增大,且 (≥0).(1)当
(≥0).(1)当 秒时,两圆的位置关系是 ;(2)当t≥4秒时,若两圆外切,则t的值为 秒.
秒时,两圆的位置关系是 ;(2)当t≥4秒时,若两圆外切,则t的值为 秒.