题目内容
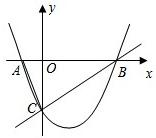
如图1,已知:抛物线y=
x2+bx+c与x轴交于A、B两点,与y轴交于点C,经过B、C两点的直线是y=
x-2,连接AC.
(1)写出B、C两点坐标,并求抛物线的解析式;
(2)判断△ABC的形状,并说明理由;
(3)若△ABC内部能否截出面积最大的矩形DEFG(顶点D、E、F、G在△ABC各边上)?若能,求出在AB边上的矩形顶点的坐标;若不能,请说明理由.
{抛物线y=ax2+bx+c的顶点坐标是(-
,
)}.
| 1 |
| 2 |
| 1 |
| 2 |
(1)写出B、C两点坐标,并求抛物线的解析式;
(2)判断△ABC的形状,并说明理由;
(3)若△ABC内部能否截出面积最大的矩形DEFG(顶点D、E、F、G在△ABC各边上)?若能,求出在AB边上的矩形顶点的坐标;若不能,请说明理由.
{抛物线y=ax2+bx+c的顶点坐标是(-
| b |
| 2a |
| 4ac-b2 |
| 4a |

(1)直线y=
x-2中,令y=0,则x=4;令x=0,则y=-2;
故B(4,0),C(0,-2);
由于抛物线经过点C(0,-2),故c=-2;
将B点坐标代入y=
x2-bx-2中,得:b=-
;
∴抛物线的解析式为y=
x2-
x-2.
(2)根据(1)中的函数解析式可知A(-1,0),B(4,0),C(0,-2);
则AB=5,AC=
,BC=2
;
故AC2+BC2=5+20=25=AB2,
∴△ABC是直角三角形,且∠ACB=90°.
(3)分两种情况考虑:
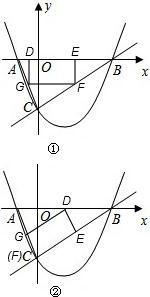
①如图①所示,矩形DEFG中D、E在AB边上;
设DG=EF=m;
由于FG∥x轴,则△CGF∽△CAB,
=
,
解得FG=5-
m;
故矩形的面积S=DG•FG=(5-
m)m=-
m2+5m,
即S=-
(m-1)2+
,
故m=1时,矩形的面积最大为2.5;
此时D(-
,0),E(2,0),G(-
,-1),F(2,-1);
②如图②所示,矩形DEFG中,F、C重合,D在AB边上;
设DE=CG=n,同①可得:
=
即DG=2
-2n;
故矩形的面积S=DE•DG=(2
-2n)n=-2(n-
)2+
;
即当n=
时,矩形的最大面积为2.5;
此时BD=5×
=
,OD=OB-BD=
,
即D(
,0);
综上所述,矩形的最大面积为2.5,此时矩形在AB边上的顶点坐标为(-
,0),(2,0)或(
,0).
| 1 |
| 2 |
故B(4,0),C(0,-2);
由于抛物线经过点C(0,-2),故c=-2;
将B点坐标代入y=
| 1 |
| 2 |
| 3 |
| 2 |
∴抛物线的解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)根据(1)中的函数解析式可知A(-1,0),B(4,0),C(0,-2);
则AB=5,AC=
| 5 |
| 5 |

故AC2+BC2=5+20=25=AB2,
∴△ABC是直角三角形,且∠ACB=90°.
(3)分两种情况考虑:
①如图①所示,矩形DEFG中D、E在AB边上;
设DG=EF=m;
由于FG∥x轴,则△CGF∽△CAB,
| 2-m |
| 2 |
| FG |
| 5 |
解得FG=5-
| 5 |
| 2 |
故矩形的面积S=DG•FG=(5-
| 5 |
| 2 |
| 5 |
| 2 |
即S=-
| 5 |
| 2 |
| 5 |
| 2 |
故m=1时,矩形的面积最大为2.5;
此时D(-
| 1 |
| 2 |
| 1 |
| 2 |
②如图②所示,矩形DEFG中,F、C重合,D在AB边上;
设DE=CG=n,同①可得:
| ||
|
| DG | ||
2
|
即DG=2
| 5 |
故矩形的面积S=DE•DG=(2
| 5 |
| ||
| 2 |
| 5 |
| 2 |
即当n=
| ||
| 2 |
此时BD=5×
| DE | ||
|
| 5 |
| 2 |
| 3 |
| 2 |
即D(
| 3 |
| 2 |
综上所述,矩形的最大面积为2.5,此时矩形在AB边上的顶点坐标为(-
| 1 |
| 2 |
| 3 |
| 2 |

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目


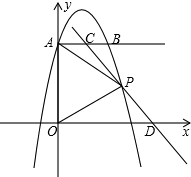 P是第一象限抛物线上一点且PA=PO,过点P的直线分别交射线AB、x正半轴于C、D.设AC=m,OD=n.
P是第一象限抛物线上一点且PA=PO,过点P的直线分别交射线AB、x正半轴于C、D.设AC=m,OD=n. 位,平移后抛物线的顶点坐标记作A,直线x=3与平移后的抛物线相交于B,与直线OA相交于C.
位,平移后抛物线的顶点坐标记作A,直线x=3与平移后的抛物线相交于B,与直线OA相交于C.

 点C(如图),点C的坐标为(0,-3),且BO=CO
点C(如图),点C的坐标为(0,-3),且BO=CO