题目内容
【题目】如图BD为△ABC的角平分线,且BD=BC, E为BD延长线上一点,BE=BA,
过E作EF⊥AB于F,下列结论:
①△ABD≌△EBC ;②∠BCE+∠BDC=180°;
③AD=AE=EC;④AB//CE ;
⑤BA+BC=2BF.其中正确的是________________.
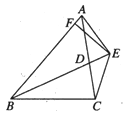
【答案】①②③⑤
【解析】①∵BD为△ABC的角平分线,∴∠ABD=∠CBD,
∴在△ABD和△EBC中, 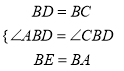 ,
,
∴△ABD≌△EBC(SAS),故①正确;
②∵BD为△ABC的角平分线,BD=BC,BE=BA,
∴∠BCD=∠BDC=∠BAE=∠BEA,
∵△ABD≌△EBC,∴∠BCE=∠BDA,
∴∠BCE+∠BCD=∠BDA+∠BDC=180°,故②正确;
③∵∠BCE=∠BDA,∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,∠BCD=∠BEA,
∴∠DCE=∠DAE,
∴△ACE为等腰三角形,
∴AE=EC,
∵△ABD≌△EBC,
∴AD=EC,
∴AD=AE=EC,故③正确;
⑤过E作EG⊥BC于G点,

∵E是BD上的点,∴EF=EG,
∵在RT△BEG和RT△BEF中, ![]() ,
,
∴RT△BEG≌RT△BEF(HL),
∴BG=BF,
∵在RT△CEG和RT△AFE中, ![]() ,
,
∴RT△CEG≌RT△AFE(HL),
∴AF=CG,
∴BA+BC=BF+FA+BGCG=BF+BG=2BF,故⑤正确;
无法证明④正确.
故答案为:①②③⑤.

练习册系列答案
相关题目